题目内容
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为
,命中得1分,没有命中得-1分;向乙靶射击两次,每次命中的概率为
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击,则该射手得3分的概率为 .
| 3 |
| 4 |
| 2 |
| 3 |
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:该射手得3分的情况有两种:①甲靶命中,乙靶两次射击命中一次;②甲靶不中,乙靶两次全中.由此能求出结果.
解答:
解:该射手得3分的情况有两种:
①甲靶命中,乙靶两次射击命中一次,
概率为p1=
×
•
•(1-
)=
.
②甲靶不中,乙靶两次全中,
概率为p2=(1-
)•(
)2=
.
∴该射手得3分的概率为:
p=p1+p2=
+
=
.
故答案为:
.
①甲靶命中,乙靶两次射击命中一次,
概率为p1=
| 3 |
| 4 |
| C | 1 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
②甲靶不中,乙靶两次全中,
概率为p2=(1-
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 9 |
∴该射手得3分的概率为:
p=p1+p2=
| 1 |
| 3 |
| 1 |
| 9 |
| 4 |
| 9 |
故答案为:
| 4 |
| 9 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
不等式x2-3x+2>0的解集为( )
| A、(-∞,-2)∪(-1,+∞) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(1,2) |
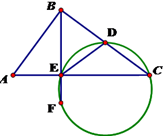 如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为
如图,在△ABC中,AB=3,BC=4,CA=5,D是BC的中点,BE⊥AC于E,BE的延长线交△DEC的外接圆于F,则EF的长为