题目内容
10个位置，现在6个人来坐，若A、B相邻，C、D相邻，E、F相邻，则共有不同的坐法 种．
考点：计数原理的应用
专题：排列组合
分析：根据题意，先排相邻的，用捆绑法，再从中选择3个位置，有分步计数原理，可得答案，
解答：
解：第一步，A、B相邻，C、D相邻，E、F相邻，故相邻的坐法有
•
=8种，
第二步，相邻的看作一个座位，相当于有7个座位供选择，有
=35种，
根据分步计数原理得，共有不同的坐法6×35=210种
故答案为：210．
| A | 2 2 |
| A | 2 2 |
| •A | 2 2 |
第二步，相邻的看作一个座位，相当于有7个座位供选择，有
| C | 3 7 |
根据分步计数原理得，共有不同的坐法6×35=210种
故答案为：210．
点评：本题主要考查了分步计数原理，相邻的问题用捆绑法，属于中档题．
练习册系列答案
相关题目
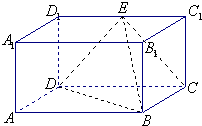长方体ABCD-A1B1C1D1的侧棱AA1=a，AB=2a，AA1=BC=a的矩形，E为C1D1的中点．
如图，在斜三棱柱ABC-A1B1C1中，O是AC的中点，A1O⊥平面ABC，∠BCA=90°，AA1=AC=BC．
如图，在正方体ABCD-A1B1C1D1中，E、F分别为AD1，CD1中点．
设数列{an}是集合{3s+3t|0≤s＜t，且s，t∈Z}中所有的数从小到大排列成的数列，即a1=4，a2=10，a3=12，a4=28，a5=30，a6=36，…，将数列{an}中各项按照上小下大，左小右大的原则排成如下等腰直角三角形数表如图，a200=