题目内容
用0,1,2,3,4,5六个数字排成没有重复数字的六位数:
(1)若0与1之间恰有两个数,则这样的六位数有多少个?
(2)若1不在个位,则这样的六位数有多少个?
(3)若这个六位数中的偶数数字从左向右从小到大排列,则这样的六位数有多少个?
(1)若0与1之间恰有两个数,则这样的六位数有多少个?
(2)若1不在个位,则这样的六位数有多少个?
(3)若这个六位数中的偶数数字从左向右从小到大排列,则这样的六位数有多少个?
考点:计数原理的应用
专题:应用题,排列组合
分析:(1)根据0与1之间恰有两个数,分类讨论,即可求得结论;
(2)首位是1时,有
种方法,首位不是1时,有
种方法,可得结论;
(3)不考虑特殊数0,有
种方法,0在首位,有
种方法,可得结论.
(2)首位是1时,有
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
(3)不考虑特殊数0,有
| A | 3 6 |
| A | 2 5 |
解答:
解:(1)0与1之间恰有两个数,若形式为1××0××,则有
=24;形式为×1××0×,则有
=24;形式为××1××0,则有
=24;形式为×0××1×,则有
=24;形式为××0××1,则有
=24,
故共有24×5=120种;
(2)首位是1时,有
种方法,首位不是1时,有
种方法,共有
+
=504种方法;
(3)不考虑特殊数0,有
种方法,0在首位,有
种方法,共有
-
=60种方法.
| A | 2 4 |
| A | 2 2 |
| A | 1 4 |
| A | 2 3 |
| A | 2 4 |
| A | 2 2 |
| A | 1 4 |
| A | 2 3 |
| A | 2 4 |
| A | 2 2 |
故共有24×5=120种;
(2)首位是1时,有
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
| A | 5 5 |
| C | 1 4 |
| C | 1 4 |
| A | 4 4 |
(3)不考虑特殊数0,有
| A | 3 6 |
| A | 3 5 |
| A | 3 6 |
| A | 3 5 |
点评:本题考查排列、组合的应用,解题时注意题干条件对数的限制,其次还要注意首位数字不能为0.

练习册系列答案
相关题目
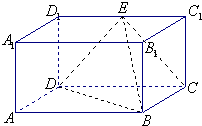 长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点.
长方体ABCD-A1B1C1D1的侧棱AA1=a,AB=2a,AA1=BC=a的矩形,E为C1D1的中点. 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC. 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.