题目内容
在△ABC中,(
a-c)cosB=bcosC,cos2A+1-
cosA=0,则tan(
+A)= .
| 2 |
| 8 |
| 5 |
| π |
| 4 |
考点:二倍角的余弦,两角和与差的正切函数
专题:三角函数的求值
分析:根据三角函数的倍角公式进行化简即可.
解答:
解:由正弦定理得:(
sinA-sinC)cosB=sinBcosC
∴
sinAcosB-sinCcosB=sinBcosC,
即
sinAcosB=sinBcosC+sinCcosB,
∴
sinAcosB=sin(B+C),
∵在△ABC中sin(B+C)=sinA,
∴
sinAcosB=sinA,
∴cosB=
,B=
,
∵cos2A+1-
cosA=0,
∴2cos2A-1+1-
cosA=0,
即2cos2A-
cosA=0,
解得cosA=0或cosA=
,
若cosA=0,则A=
,
则tan(
+A)=tan
=-1,
若cosA=
,则sinA=
,则tanA=
,
则tan(
+A)=
=
=7,
故答案为:7或-1
| 2 |
∴
| 2 |
即
| 2 |
∴
| 2 |
∵在△ABC中sin(B+C)=sinA,
∴
| 2 |
∴cosB=
| ||
| 2 |
| π |
| 4 |
∵cos2A+1-
| 8 |
| 5 |
∴2cos2A-1+1-
| 8 |
| 5 |
即2cos2A-
| 8 |
| 5 |
解得cosA=0或cosA=
| 4 |
| 5 |
若cosA=0,则A=
| π |
| 2 |
则tan(
| π |
| 4 |
| 3π |
| 4 |
若cosA=
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 4 |
则tan(
| π |
| 4 |
| 1+tanA |
| 1-tanA |
1+
| ||
1-
|
故答案为:7或-1
点评:本题主要考查三角函数式子的化简,利用三角函数的倍角公式以及正弦定理是解决本题的关键.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
以椭圆
+
=1的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、y2=-4x |
| B、y2=-2x |
| C、y2=-8x |
| D、y=-x |
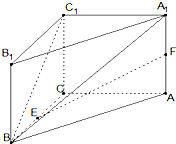 在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.
在直三棱柱ABC-A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BC A1A的中点.