题目内容
若f(x)=
在(0,+∞)上有极值时,求a的范围.
| 2x2-ax+1 |
| x |
考点:利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:由题意求导f′(x)=2-
=
;从而可得f(x)=
在(0,+∞)上在x=
处有极小值,从而解得.
| 1 |
| x2 |
| 2x2-1 |
| x2 |
| 2x2-ax+1 |
| x |
| ||
| 2 |
解答:
解:f(x)=
=2x+
-a;
f′(x)=2-
=
;
故f(x)在(0,
)上是减函数,
在(
,+∞)上是增函数;
故f(x)=
在(0,+∞)上在x=
处有极小值,
故a∈R.
| 2x2-ax+1 |
| x |
| 1 |
| x |
f′(x)=2-
| 1 |
| x2 |
| 2x2-1 |
| x2 |
故f(x)在(0,
| ||
| 2 |
在(
| ||
| 2 |
故f(x)=
| 2x2-ax+1 |
| x |
| ||
| 2 |
故a∈R.
点评:本题考查了导数的综合应用,同时考查了极值的条件.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
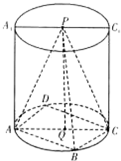 如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC.
如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC. 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CC1的中点,求异面直线AE和BF所成角的余弦值.