题目内容
已知f(x)=2mcos2x-2
msinx•cosx+n(m>0)的定义域为[0,
],值域为[1,4],求m+n的值.
| 3 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:利用二倍角公式和两角和公式对函数解析式化简整理,进而根据x的范围表示出f(x)的最大和最小值,联立方程求得m和n,最后求得m+n的值.
解答:
解:f(x)=2mcos2x-2
msinx•cosx+n
=m(1+cos2x-
sin2x)+n
=2m(
cos2x-
sin2x)+m+n,
=-2msin(2x-
)+m+n,
∵x∈[0,
],
∴-
≤2x-
≤
,
∴-
≤sin(2x-
)≤1,
∴f(x)max=-2•m•(-
)+m+n=4①
f(x)min=-2m+m+n=1②,
①②联立求得n=4,m=3,
∴m+n=7
| 3 |
=m(1+cos2x-
| 3 |
=2m(
| 1 |
| 2 |
| ||
| 2 |
=-2msin(2x-
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴f(x)max=-2•m•(-
| 1 |
| 2 |
f(x)min=-2m+m+n=1②,
①②联立求得n=4,m=3,
∴m+n=7
点评:本题主要考查了三角函数的恒等变换,三角函数的图象和性质.考查了学生综合运用三角函数基础知识的能力和运算的能力.

练习册系列答案
相关题目
已知a,b∈[-1,1],则函数f(x)=ax+b在区间(1,2)上存在一个零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x,y满足不等式组
,则2x+3y的最大值等于( )
|
| A、1 | B、10 | C、41 | D、50 |
定义在R上的函数f(x)=
,则f(2013)=( )
|
| A、1 | B、2 | C、-2 | D、-3 |
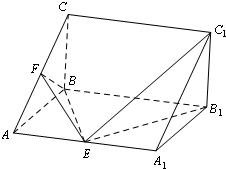 如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=
如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=