题目内容
某射击测试规则为:每人最多射击3次,击中目标即终止射击,第i次射击击中目标得i(i=1,2,3)分,3次均击中目标得0分.已知某射手每次击中目标的概率为0.8,各次射击结果互不影响.
(Ⅰ)求该射手至少射击两次并且击中目标的概率;
(Ⅱ)记该射手的得分为ξ,求随机变量ξ的分布列及数学期望.
(Ⅰ)求该射手至少射击两次并且击中目标的概率;
(Ⅱ)记该射手的得分为ξ,求随机变量ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:对于(Ⅰ)求该射手至少射击两次并且击中目标,因为击中目标即终止射击,则该射手第一次没有射中第二次射中或者第一、二次没有射中第三次射中,根据相互独立事件的概率乘法公式即可直接求得答案.
对于(Ⅱ)该射手的得分记为ξ,求ξ的分布列及数学期望,因为第i次击中目标得1~i(i=1,2,3)分,故ξ可能取的值为0,1,2,3.分别求出每个值的概率,填入分布列表,然后根据期望公式求得期望即可.
对于(Ⅱ)该射手的得分记为ξ,求ξ的分布列及数学期望,因为第i次击中目标得1~i(i=1,2,3)分,故ξ可能取的值为0,1,2,3.分别求出每个值的概率,填入分布列表,然后根据期望公式求得期望即可.
解答:
解:(Ⅰ)设该射手第i次击中目标的事件为Ai(i=1,2,3),
则P(Ai)=0.8,P(
)=0.2,
∴该射手至少射击两次并且击中目标的概率为P(
A2)+P(
A3)=0.2×0.8+0.2×0.2×0.8=0.192;
(Ⅱ)ξ可能取的值为0,1,2,3.
ξ的分布列为:
Eξ=0×0.008+1×0.8+2×0.16+3×0.032=1.216.
则P(Ai)=0.8,P(
. |
| Ai |
∴该射手至少射击两次并且击中目标的概率为P(
. |
| A1 |
. |
| A1 |
. |
| A2 |
(Ⅱ)ξ可能取的值为0,1,2,3.
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.8 | 0.16 | 0.032 |
点评:本题考查相互独立事件的概率乘法公式,考查离散型随机变量的数学期望的求法,属于中档题.

练习册系列答案
相关题目
对任意两实数a,b,定义运算“*”:a*b=
,关于函数f(-x)=e-x*ex,给出下列四个结论:
①函数f(x)的最小值是e;
②函数f(x)为偶函数;
③函数f(x)在(0,+∞)上单调递增;
④函数f(x)的图象与直线y=ex没有公共点;
其中正确结论的序号是( )
|
①函数f(x)的最小值是e;
②函数f(x)为偶函数;
③函数f(x)在(0,+∞)上单调递增;
④函数f(x)的图象与直线y=ex没有公共点;
其中正确结论的序号是( )
| A、①③ | B、②③ | C、①④ | D、②④ |
已知等差数列{an}满足a1+a5=20且a9=20,则a15=( )
| A、15 | B、20 | C、25 | D、30 |
 如图1,△ABC为正三角形,△BCD为等腰直角三角形,∠BCD=90°,将△ABC沿BC边折叠到△A′BC的位置,使A′B=A′D,E为BD中点,如图2.
如图1,△ABC为正三角形,△BCD为等腰直角三角形,∠BCD=90°,将△ABC沿BC边折叠到△A′BC的位置,使A′B=A′D,E为BD中点,如图2.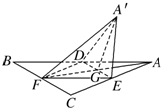 如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: 数字1,2,3,…,9这九个数字填写在如图的9个空格中,要求每一行从左到右依次增大,每列从上到下也依次增大,当数字4固定在中心位置时,则所有填写空格的方法共有
数字1,2,3,…,9这九个数字填写在如图的9个空格中,要求每一行从左到右依次增大,每列从上到下也依次增大,当数字4固定在中心位置时,则所有填写空格的方法共有