Question

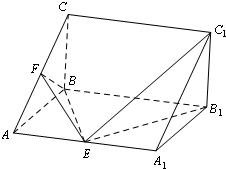如图，在三菱柱ABC-A₁B₁C₁中，AA₁B₁B为矩形，平面AA₁B₁B⊥平面ABC．∠ABC=90°，AB=BC=

1

2

AA₁=1，点F为AC的中点，点E为AA₁上一点．
（1）求证：平面BEF⊥平面AA₁C₁C；
（2）当AE的长为何值时，二面角A₁-C₁E-B₁为60°？

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面垂直的判定

专题：空间角

分析：（1）由已知条件推导出BF⊥AC，BF⊥AA₁，由此能证明平面BEF⊥平面AA₁C₁C．
（2）以B为原点，以BA为x轴，以BB₁为y轴，以BC为z轴，建立空间直角坐标系，利用向量法能求出当AE=

1

2

AA1=1时，二面角A₁-C₁E-B₁为60°．

解答： （1）证明：∵在三菱柱ABC-A₁B₁C₁中，AA₁B₁B为矩形，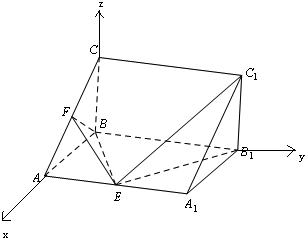
平面AA₁B₁B⊥平面ABC．∠ABC=90°，
∴BF⊥AC，
又∵AA₁⊥平面ABC，BF?平面ABC，
∴BF⊥AA₁，
∵AC∩AA₁=A，∴BF⊥平面AA₁C₁C，
∵BF?平面BEF，
∴平面BEF⊥平面AA₁C₁C．
（2）解：以B为原点，以BA为x轴，以BB₁为y轴，以BC为z轴，建立空间直角坐标系，
∵AB=BC=

1

2

AA₁=1，点F为AC的中点，点E为AA₁上一点
∴设AE=λAA₁时，二面角A₁-C₁E-B₁为60°．
A（1，0，0），A₁（1，2，0），则E（1，2λ，0），C₁（0，2，1），B₁（0，2，0），
∴

C1A1

=（1，0，-1），

C1E

=（1，2λ-2，-1），

C1B1

=（0，0，-1），
设平面C₁A₁E的法向量

n

=（x，y，z），
则

n • C1A1 =x-z=0 n • C1E =x+(2λ-2)y-z=0

，取x=1，得

n

=(1，0，1)，
设平面C₁EB₁的法向量

m

=(a，b，c)，
则

m • C1E =a+(2λ-2)b-c=0 m • C1B1 =-c=0

，取a=1，得

m

=(1，

1

2-2λ

，0)，
∵二面角A₁-C₁E-B₁为60°，
∴cos60°=

1

2 • 1+( 1 2-2λ )2

，解得λ=

1

2

或λ=

3

2

（舍），
∴当AE=

1

2

AA1=1时，二面角A₁-C₁E-B₁为60°．

点评：本题考查平面与平面垂直的证明，考查二面角为60°时点的位置的确定，解题时要认真审题，注意向量法的合理运用．