题目内容
如果数列{an}同时满足:(1)各项均不为0,(2)存在常数k,对任意n∈N*,an+12anan+2+k都成立,则称这样的数列{an}为“类等比数列”.由此等比数列必定是“类等比数列”.问:
(1)各项均不为0的等差数列{bn}是否为“类等比数列”?说明理由.
(2)若数列{an}为“类等比数列”,且a1=a,a2=b(a,b为常数),是否存在常数λ,使得an+an+2=λan+1对任意n∈N*都成立?若存在,求出λ;若不存在,请举出反例.
(3)若数列{an}为“类等比数列”,且a1=a,a2=b,k=a2+b2(a,b为常数),求数列{an}的前n项之和Sn;数列{Sn}的前n项之和记为Tn,求T4k-3(k∈N*).
(1)各项均不为0的等差数列{bn}是否为“类等比数列”?说明理由.
(2)若数列{an}为“类等比数列”,且a1=a,a2=b(a,b为常数),是否存在常数λ,使得an+an+2=λan+1对任意n∈N*都成立?若存在,求出λ;若不存在,请举出反例.
(3)若数列{an}为“类等比数列”,且a1=a,a2=b,k=a2+b2(a,b为常数),求数列{an}的前n项之和Sn;数列{Sn}的前n项之和记为Tn,求T4k-3(k∈N*).
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)因为{bn}为各项均不为0的等差数列,故可设bn=dn+b(d、b为常数),利用“类等比数列”的定义,可得k=d2为常数,即可得出结论;
(2)存在常数λ=
,使an+an+2=λan+1,再进行证明即可;
(3){a2n-1},{a2n}均为公比为-1的等比数列,可求Sn、Tn,即可求T4k-3(k∈N*).
(2)存在常数λ=
| a2+b2-k |
| ab |
(3){a2n-1},{a2n}均为公比为-1的等比数列,可求Sn、Tn,即可求T4k-3(k∈N*).
解答:
解:(1)因为{bn}为各项均不为0的等差数列,故可设bn=dn+b(d、b为常数) …(1分)
由bn+12=bnbn+2+k得[d(n+1)+b]2=(dn+b)[d(n+2)+b]+k…(2分)
得k=d2为常数,所以各项均不为0的等差数列{bn}为“类等比数列”…(4分)
(2)存在常数λ=
,使an+an+2=λan+1(只给出结论给2分)
(或从必要条件入手a1+a3=λa2⇒λ=
=
=
)
证明如下:因为
=anan+2+k,所以
=an-1an+1+k,n≥2,n∈N*
所以
-
=anan+2-an-1an+1,即
+an-1an+1=anan+2+
.…(6分)
由于an≠0,此等式两边同除以anan+1,
得
=
…(8分)
所以
=
=…=
,
即当n∈N*都有an+an+2=
an+1
因为a1=a,a2=b,
=anan+2+k,所以a3=
所以
=
=
•
所以对任意n∈N*都有an+an+2=λan+1,此时λ=
…(10分)
(3)a22=a1a3+k=a1a3+a12+a22⇒a1(a1+a3)=0⇒a1+a3=0…(11分)
=
=…=
=0⇒an+an+2=0,
∴{a2n-1},{a2n}均为公比为-1的等比数列 …(12分)
∴an=
…(14分)
Sn=
(k∈N*)…(16分)
T4k-3=T4k-S4k-S4k-1-S4k-2=2(a+b)k-0-b-(a+b)=2(a+b)(k-1)+a(18分)
由bn+12=bnbn+2+k得[d(n+1)+b]2=(dn+b)[d(n+2)+b]+k…(2分)
得k=d2为常数,所以各项均不为0的等差数列{bn}为“类等比数列”…(4分)
(2)存在常数λ=
| a2+b2-k |
| ab |
(或从必要条件入手a1+a3=λa2⇒λ=
| a1+a3 |
| a2 |
a1+
| ||
| a2 |
| a2+b2-k |
| ab |
证明如下:因为
| a | 2 n+1 |
| a | 2 n |
所以
| a | 2 n+1 |
| a | 2 n |
| a | 2 n+1 |
| a | 2 n |
由于an≠0,此等式两边同除以anan+1,
得
| an+an+2 |
| an+1 |
| an-1+an+1 |
| an |
所以
| an+an+2 |
| an+1 |
| an-1+an+1 |
| an |
| a1+a3 |
| a2 |
即当n∈N*都有an+an+2=
| a1+a3 |
| a2 |
因为a1=a,a2=b,
| a | 2 n+1 |
| b2-k |
| a |
所以
| a1+a3 |
| a2 |
a+
| ||
| b |
| a2+b2-k |
| ab |
所以对任意n∈N*都有an+an+2=λan+1,此时λ=
| a2+b2-k |
| ab |
(3)a22=a1a3+k=a1a3+a12+a22⇒a1(a1+a3)=0⇒a1+a3=0…(11分)
| an+an+2 |
| an+1 |
| an-1+an+1 |
| an |
| a1+a3 |
| a2 |
∴{a2n-1},{a2n}均为公比为-1的等比数列 …(12分)
∴an=
|
Sn=
|
T4k-3=T4k-S4k-S4k-1-S4k-2=2(a+b)k-0-b-(a+b)=2(a+b)(k-1)+a(18分)
点评:本题考查数列的应用,考查新定义,考查数列的通项与求和,考查学生分析解决问题的能力,正确运用新定义是关键.

练习册系列答案
相关题目
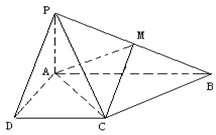 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=