题目内容
已知sinα,cosα是方程2x2-x-m=0的两个根,则m的值是多少?
考点:根与系数的关系
专题:计算题,三角函数的求值
分析:由sinα,cosα是方程2x2-x-m=0的两个根,根据韦达定理(一元二次方程根与系数的关系)我们易得:sinα+cosα=
,sinα•cosα=-
,结合同角三角函数平方关系,根据一个关于m的方程,解方程即可得到答案.
| 1 |
| 2 |
| m |
| 2 |
解答:
解:∵sinα,cosα是方程2x2-x-m=0的两个根,
∴sinα+cosα=
,sinα•cosα=-
,
则(sinα+cosα)2
=1+2sinα•cosα
=1-m=
,
∴m=
∴sinα+cosα=
| 1 |
| 2 |
| m |
| 2 |
则(sinα+cosα)2
=1+2sinα•cosα
=1-m=
| 1 |
| 4 |
∴m=
| 3 |
| 4 |
点评:本题考查的知识点是一元二次方程根与系数的关系(韦达定理)及同角三角函数关系,其中根据sinα,cosα是方程2x2-x-m=0的两个根,结合韦达定理,得到sinα+cosα=
,sinα•cosα=-
,进而将问题转化为一个三角函数给值求值问题是解答本题的关键.
| 1 |
| 2 |
| m |
| 2 |

练习册系列答案
相关题目
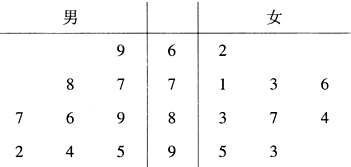 某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.
某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示. 如图是某公司10个销售店某月销售某品牌电脑数量(单位:台)的茎叶图,则数
如图是某公司10个销售店某月销售某品牌电脑数量(单位:台)的茎叶图,则数