题目内容

甲地区有10名人大代表，其中有4名女性；乙地区有5名人大代表，其中有3名女性，现采用分层抽样法从甲、乙两地区共抽取3名代表进行座谈．
（Ⅰ）求从甲、乙两地区各抽取的代表数；
（Ⅱ）求从甲组抽取的代表中至少有1名女性的概率；
（Ⅲ）记ξ表示抽取的3名代表中女性数，求ξ的分布列及数学期望．
考点：离散型随机变量的期望与方差,分层抽样方法,古典概型及其概率计算公式
专题：计算题,概率与统计
分析：（Ⅰ）根据分层抽样，可得结论；
（Ⅱ）利用等可能事件概率公式可求从甲组抽取的代表中至少有1名女性的概率；
（Ⅲ）确定ξ的可能取值，求出相应的概率，即可求得ξ的分布列及数学期望．
解答： 解：（Ⅰ）甲地区有10名人大代表，其中有4名女性；乙地区有5名人大代表，其中有3名女性，
∴采用分层抽样，应在甲地区抽去2人，乙地区抽取1人…（2分）
（Ⅱ）P=
C
1
6
C
1
4
C
2
10
+
C
2
4
C
2
10
=
2
3
，
∴从甲组抽取的代表中至少有1名女性的概率为
2
3
．…（5分）
（Ⅲ）依据题意得ξ可取0、1、2、3．
由P（ξ=0）=
C
2
6
C
1
2
C
2
10
C
1
5
=
2
15
…（6分）P（ξ=1）=
C
2
6
C
1
3
+
C
1
6
C
1
4
C
1
2
C
2
10
C
1
5
=
31
75
…（7分）
P（ξ=2）=
C
2
4
C
1
2
+
C
1
6
C
1
4
C
1
3
C
2
10
C
1
5
=
28
75
； P(ξ=3)=
C
2
4
C
1
3
C
2
10
C
1
5
=
6
75
…（9分）
 ξ01 23
 P
2
15
31
75
28
75
6
75
∴Eξ=0×
2
15
+1×
31
75
+2×
28
75
+3×
6
75
=1.4．
点评：本题考查分层抽样，考查对立事件的概率，考查离散型随机变量的分布列与期望，确定ξ的可能取值，求出相应的概率是关键．
练习册系列答案
相关题目
已知F1，F2为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，过椭圆右焦点F2斜率为k（k≠0）的直线l与椭圆C相交于E、F两点，△EFF1的周长为8，且椭圆C与圆x2+y2=3相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设A为椭圆的右顶点，直线AE，AF分别交直线x=4于点M，N，线段MN的中点为P，记直线PF2的斜率为k′，求证k•k′为定值．
为了构建和谐社会建立幸福指标体系，某地区决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）．
相关人员数 抽取人数
公务员 32 m
教师 16 n
自由职业者 64 8
（Ⅰ）求研究小组的总人数；
（Ⅱ）若从研究小组的公务员和教师中随机选3人撰写研究报告，求其中恰好有1人来自教师的概率．
一个袋中装有大小相同的黑球和白球共9个，从中任取2个球，记随机变量X为取出2球中白球的个数，已知P（X=2）=
5
12
．
（Ⅰ）求袋中白球的个数；
（Ⅱ）求随机变量X的分布列及其数学期望．
（1）证明：xlnx≥x-1；
（2）讨论函数f（x）=ex-ax-1的零点个数．
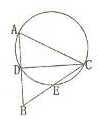已知，在△ABC中，D是AB上一点，△ACD的外接圆交BC于点E，AB=2BE．
（Ⅰ）求证：BC=2BD；
（Ⅱ）若CD平分∠ACB，且AC=2，EC=1，求BD的长．
如果数列{an}同时满足：（1）各项均不为0，（2）存在常数k，对任意n∈N*，an+12anan+2+k都成立，则称这样的数列{an}为“类等比数列”．由此等比数列必定是“类等比数列”．问：
（1）各项均不为0的等差数列{bn}是否为“类等比数列”？说明理由．
（2）若数列{an}为“类等比数列”，且a1=a，a2=b（a，b为常数），是否存在常数λ，使得an+an+2=λan+1对任意n∈N*都成立？若存在，求出λ；若不存在，请举出反例．
（3）若数列{an}为“类等比数列”，且a1=a，a2=b，k=a2+b2（a，b为常数），求数列{an}的前n项之和Sn；数列{Sn}的前n项之和记为Tn，求T4k-3（k∈N*）．
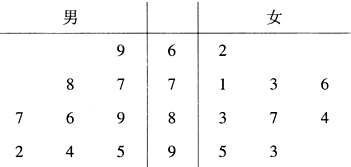某中学招聘教师有笔试、面试两个环节，笔试成绩超过85分者才能进入面试环节，现已记录前来应聘的9位男教师和9位女教师的笔试成绩，成绩用茎叶图表示如图所示．
（Ⅰ）求男教师的平均成绩和女教师成绩的中位数；
（Ⅱ）从进入面试环节的老师中随机挑选2位老师，求2位老师中至少有一位男教师的概率．
某班50位同学，期中考试成绩全部落在[90，150]上，将成绩分成6组：[90，100），[100，110），[110，120），[120，130），[130，140），[140，150]，加以统计，得到如图所示的部分频率分布直方图．
（Ⅰ）求成绩在[110，120）上的学生人数，并将频率分布直方图补充完整；
（Ⅱ）从成绩不低于130的学生中随机抽取两名，求至少一名学生的成绩不低于140的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网