题目内容
已知函数f(x)=[ax2+(a-1)2x+a-(a-1)2]ex(其中a∈R).
(Ⅰ)若x=0为f(x)的极值点,求a的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式f(x)>(x-1)(
x2+x+1);
(Ⅲ)若函数f(x)在区间(1,2)上单调递增,求实数a的取值范围.
(Ⅰ)若x=0为f(x)的极值点,求a的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式f(x)>(x-1)(
| 1 |
| 2 |
(Ⅲ)若函数f(x)在区间(1,2)上单调递增,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)利用导数求极值,由x=0为f(x)的极值点得,f′(0)=ae0=0,即得a的值;
(2)由不等式f(x)>(x-1)(
x2+x+1)得,(x-1)[ex-(
x2+x+1)]>0,利用导数判断函数g(x)=)ex-(
x2+x+1)的单调性,进而得证;
(3)由导数与函数单调性的关系,通过讨论求得a的范围.
(2)由不等式f(x)>(x-1)(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由导数与函数单调性的关系,通过讨论求得a的范围.
解答:
解:(Ⅰ)因为f(x)=[ax2+(a-1)2x+a-(a-1)2]ex
所以f′(x)=[2ax+(a-1)2]ex+[ax2+(a-1)2x+a-(a-1)2]ex=[ax2+(a2+1)x+a]ex--------(2分)
因为x=0为f(x)的极值点,所以由f′(0)=ae0=0,解得a=0----------------------------(3分)
检验,当a=0时,f′(x)=xex,当x<0时,f′(x)<0,当x>0时,f′(x)>0,
所以x=0为f(x)的极值点,故a=0.----------------------------------------(4分)
(Ⅱ) 当a=0时,不等式不等式f(x)>(x-1)(
x2+x+1)?(x-1)ex>(x-1)(
x2+x+1),
整理得(x-1)[ex-(
x2+x+1)]>0,
即
或
------------(6分)
令g(x)=)ex-(
x2+x+1),h(x)=g′(x)=ex-(x+1),h′(x)=ex-1,
当x>0时,h′(x)=ex-1>0,当x<0时,h′(x)=ex-1<0,
所以h(x)在(-∞,0)单调递减,在(0,+∞)单调递增,
所以h(x)>h(0)=0,即g′(x)>0,
所以g(x)在R上单调递增,而g(0)=0;
故ex-(
x2+x+1)>0?x>0;ex-(
x2+x+1)<0?x<0,
所以原不等式的解集为{x|x<0或x>1};-------------------------(9分)
(Ⅲ) 当a≥0时,f′(x)=[ax2+(a2+1)x+a]ex,
因为x∈(1,2),所以f′(x)>0,所以f(x)在(1,2)上是增函数.----------(11分)
当a<0时,f′(x)=a(x+a)(x+
)•ex,x∈(1,2)时,f(x)是增函数,f′(x)>0.
①若a<-1,则f′(x)=a(x+a)(x+
)•ex>0⇒x∈(-
,-a),由(1,2)⊆(-
,-a)得a≤-2;
②若-1<a<0,则f′(x)=a(x+a)(x+
)•ex>0⇒x∈(-a,-
),由(1,2)⊆(-a,-
)得-
≤a<0.
③若a=-1,f′(x)=-(x-1)2•ex≤0,不合题意,舍去.
综上可得,实数a的取值范围是(-∞,-2]∪[-
,+∞)----------------(14分)
所以f′(x)=[2ax+(a-1)2]ex+[ax2+(a-1)2x+a-(a-1)2]ex=[ax2+(a2+1)x+a]ex--------(2分)
因为x=0为f(x)的极值点,所以由f′(0)=ae0=0,解得a=0----------------------------(3分)
检验,当a=0时,f′(x)=xex,当x<0时,f′(x)<0,当x>0时,f′(x)>0,
所以x=0为f(x)的极值点,故a=0.----------------------------------------(4分)
(Ⅱ) 当a=0时,不等式不等式f(x)>(x-1)(
| 1 |
| 2 |
| 1 |
| 2 |
整理得(x-1)[ex-(
| 1 |
| 2 |
即
|
|
令g(x)=)ex-(
| 1 |
| 2 |
当x>0时,h′(x)=ex-1>0,当x<0时,h′(x)=ex-1<0,
所以h(x)在(-∞,0)单调递减,在(0,+∞)单调递增,
所以h(x)>h(0)=0,即g′(x)>0,
所以g(x)在R上单调递增,而g(0)=0;
故ex-(
| 1 |
| 2 |
| 1 |
| 2 |
所以原不等式的解集为{x|x<0或x>1};-------------------------(9分)
(Ⅲ) 当a≥0时,f′(x)=[ax2+(a2+1)x+a]ex,
因为x∈(1,2),所以f′(x)>0,所以f(x)在(1,2)上是增函数.----------(11分)
当a<0时,f′(x)=a(x+a)(x+
| 1 |
| a |
①若a<-1,则f′(x)=a(x+a)(x+
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
②若-1<a<0,则f′(x)=a(x+a)(x+
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
③若a=-1,f′(x)=-(x-1)2•ex≤0,不合题意,舍去.
综上可得,实数a的取值范围是(-∞,-2]∪[-
| 1 |
| 2 |
点评:本题主要考查利用导数研究函数的单调性、极值等知识,考查分类讨论等数学思想的运用能力,属难题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
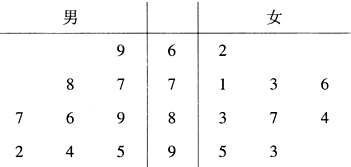 某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.
某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示. 某班50位同学,期中考试成绩全部落在[90,150]上,将成绩分成6组:[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],加以统计,得到如图所示的部分频率分布直方图.
某班50位同学,期中考试成绩全部落在[90,150]上,将成绩分成6组:[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],加以统计,得到如图所示的部分频率分布直方图.