题目内容
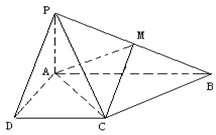 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 |
| 2 |
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小余弦值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明面PAD⊥面PCD,只需证明面PCD内的直线CD,垂直平面PAD内的两条相交直线AD、PD即可;
(Ⅱ)过点B作BE∥CA,且BE=CA,∠PBE是AC与PB所成的角,解直角三角形PEB求AC与PB所成的角;
(Ⅲ)作AN⊥CM,垂足为N,连接BN,说明∠ANB为所求二面角的平面角,在三角形AMC中,用余弦定理求面AMC与面BMC所成二面角的大小.
(Ⅱ)过点B作BE∥CA,且BE=CA,∠PBE是AC与PB所成的角,解直角三角形PEB求AC与PB所成的角;
(Ⅲ)作AN⊥CM,垂足为N,连接BN,说明∠ANB为所求二面角的平面角,在三角形AMC中,用余弦定理求面AMC与面BMC所成二面角的大小.
解答:
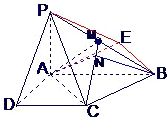 (Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD?面PCD,
∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE∥CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=
,又AB=2,
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=a2=3b2,PB=
,
∴cos∠PBE=
.
∴AC与PB所成的角为arccos
.
(Ⅲ)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN•MC=
,
∴AN=
.
∴AB=2,
∴cos∠ANB=
=-
故面AMC与面BMC所成二面角的大小余弦值为-
.
 (Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD?面PCD,
∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE∥CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=
| 2 |
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=a2=3b2,PB=
| 5 |
∴cos∠PBE=
| ||
| 5 |
∴AC与PB所成的角为arccos
| ||
| 5 |
(Ⅲ)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN•MC=
CM2-(
|
∴AN=
| ||
| 5 |
∴AB=2,
∴cos∠ANB=
| AN2+BN2-AB3 |
| 2AN×BN |
| 2 |
| 3 |
故面AMC与面BMC所成二面角的大小余弦值为-
| 2 |
| 3 |
点评:本题考查平面与平面垂直,二面角的求法,异面直线所成的角,考查空间想象能力,逻辑思维能力,转化思想,是中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
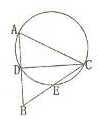 已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.
已知,在△ABC中,D是AB上一点,△ACD的外接圆交BC于点E,AB=2BE.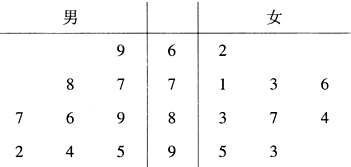 某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.
某中学招聘教师有笔试、面试两个环节,笔试成绩超过85分者才能进入面试环节,现已记录前来应聘的9位男教师和9位女教师的笔试成绩,成绩用茎叶图表示如图所示.