题目内容
3.已知函数g(x)=$\frac{{4}^{x}-a}{{2}^{x}}$是奇函数,f(x)=lg(10x+1)+bx是偶函数.(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2-2t)+g(2t2-k)>0恒成立,求实数k的取值范围.
分析 (1)根据函数奇偶性的定义建立方程进行求解即可.
(2)根据函数奇偶性和单调性的关系,将不等式进行转化求解即可.
解答 解:(1)∵g(x)=$\frac{{4}^{x}-a}{{2}^{x}}$是定义在R上的奇函数,
∴由g(0)=0得1-a=0,得a=1,
则g(x)=$\frac{{4}^{x}-1}{{2}^{x}}$,经检验g(x)是奇函数,
由f(-1)=f(1)得lg(10-1+1)-b=lg(10+1)+b,
即2b=lg($\frac{11}{10}$×$\frac{1}{11}$)=lg($\frac{1}{10}$)=-1,
即b=-$\frac{1}{2}$,则f(x)=lg(10x+1)-$\frac{1}{2}$x,经检验f(x)是偶函数
∴a+b=$\frac{1}{2}$ …(5分)(未说明检验的扣1分)
(2)∵g(x)=$\frac{{4}^{x}-1}{{2}^{x}}$=2x-$\frac{1}{{2}^{x}}$,且g(x)在(-∞,+∞)单调递增,且g(x)为奇函数.
∴由g(t2-2t)+g(2t2-k)>0恒成立,得
g(t2-2t)>-g(2t2-k)=g(-2t2+k),…(7分)
∴t2-2t>-2t2+k,在t∈[0,+∞)上恒成立
即3t2-2t>k,在t∈[0,+∞)上恒成立…(9分)
令F(x)=3t2-2t,在[0,+∞)的最小值为F($\frac{1}{3}$)=-$\frac{1}{3}$…(11分)
∴k<$-\frac{1}{3}$…(12分)
点评 本题主要考查函数奇偶性的应用,以及不等式恒成立问题,根据条件建立方程求出a,b的值以及利用函数单调性之间的关系是解决本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.直线a、b、c两两平行,但不共面,经过其中2条直线的平面共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0或有无数多个 |
14.已知集合A={-1,0,1},B={x|-1≤x≤1},则A∩B=( )
| A. | {-1,0,1} | B. | {x|-1≤x≤1} | C. | {-1,0} | D. | {0,1} |
11.已知集合A={x|-1<x<3},B={x|x>1},则集合A∩B=( )
| A. | {-1,3} | B. | {-1,1} | C. | (1,3) | D. | {-1,+∞} |
8.设P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)上一点,双曲线的一条渐近线方程为3x-2y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=5,则|PF2|=( )
| A. | 1或9 | B. | 6 | C. | 9 | D. | 以上都不对 |
15.已知二次函数y=x2+bx+c的图象过(1,0)与(3,0),则此函数的单调减区间为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
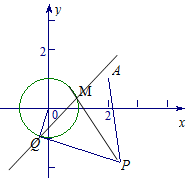 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|.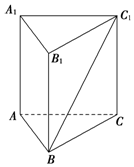 如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.