题目内容
13.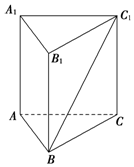 如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
如图所示,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为30°,求该三棱柱的体积.
分析 由已知找出异面直线BC1与AA1所成角,求解直角三角形得正三棱柱底面边长,再由棱柱体积公式求解.
解答 解:在正三棱柱ABC-A1B1C1中,∵CC1∥AA1.
∴∠BC1C为异面直线BC1与AA1所成的角,即∠BC1C=30°.
在Rt△BCC1中,
BC=CC1•tan∠BC1C=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
从而S△ABC=$\frac{1}{2}$BC2•sin60°=3$\sqrt{3}$,
因此该三棱柱的体积V=S△ABC•AA1=3$\sqrt{3}$×6=18$\sqrt{3}$.
点评 本题考查棱柱、棱锥、棱台的体积,考查直角三角形的解法,是基础的计算题.

练习册系列答案
相关题目
4.已知y=f(x)是定义在R上的增函数且为奇函数,若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
| A. | (3,7) | B. | (9,25) | C. | (13,49) | D. | (9,49) |
5.已知集合$A=\left\{{\left.x\right|\frac{x}{x-1}≥0,x∈R}\right\},B=\left\{{\left.y\right|y=3{x^2}+1,x∈R}\right\}$,则A∩B=( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (-∞,0]∪(1,+∞) | D. | [0,1] |
2.已知空间四边形OABC,M,N分别是对边OA,BC的中点,点G在线段MN上,且,设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x,y,z的值分别是( )
| A. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ | B. | x=$\frac{1}{3}$,y=$\frac{1}{3}$,z=$\frac{1}{6}$ | C. | x=$\frac{1}{3}$,y=$\frac{1}{6}$,z=$\frac{1}{3}$ | D. | x=$\frac{1}{6}$,y=$\frac{1}{3}$,z=$\frac{1}{3}$ |
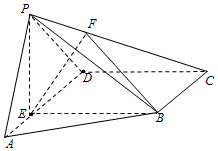 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.