题目内容
18.在公差不为零的等差数列{an}中,a1=8,且a1、a5、a7成等比数列,则Sn最大时,Sn=36.分析 设公差d不为零的等差数列{an},运用等比数列的中项性质和等差数列的通项公式,解方程可得d=-1,再由等差数列的求和公式,结合二次函数最值的求法,注意n为正整数,即可得到最大值.
解答 解:设公差d不为零的等差数列{an},
由a1=8,且a1、a5、a7成等比数列,
可得a52=a1a7,
即(8+4d)2=8(8+6d),
解得d=-1(0舍去),
则Sn=na1+$\frac{1}{2}$n(n-1)d=8n-$\frac{1}{2}$n(n-1)
=-$\frac{1}{2}$(n-$\frac{17}{2}$)2+$\frac{289}{8}$,
由于n为正整数,可知n=8或9,
则Sn最大,且为36.
故答案为:36.
点评 本题考查等差数列的通项公式和求和公式,以及等比数列的中项的性质,考查二次函数思想的运用:求最值,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.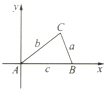 补全用解析法证明余弦定理的过程.
补全用解析法证明余弦定理的过程.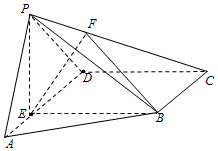 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.