题目内容
当x>1时,试比较x+lnx与e2x的大小.
考点:不等式比较大小
专题:综合题,导数的综合应用
分析:构造函数f(x)=e2x-x-lnx,利用导数判断函数在(1,+∞)上的单调性,利用函数的单调性求得函数的最值,依次可得x+lnx与e2x的大小.
解答:
解:设f(x)=e2x-x-lnx,
f′(x)=2ex-1-
,当x>1时,f′(x)>0,
∴函数f(x)=e2x-x-lnx在(1,+∞)上是增函数,
∵f(1)=e2-1-0>0,
∴f(x)=e2x-x-lnx>f(1)>0,
∴x+lnx<e2x
f′(x)=2ex-1-
| 1 |
| x |
∴函数f(x)=e2x-x-lnx在(1,+∞)上是增函数,
∵f(1)=e2-1-0>0,
∴f(x)=e2x-x-lnx>f(1)>0,
∴x+lnx<e2x
点评:本题借助不等式比较大小考查了导数的应用,熟练掌握利用导数法判断函数的单调性是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知z=(1+i)(1-mi)是纯虚数(i是虚数单位),则实数m的值为( )
| A、±1 | B、1 | C、2 | D、-1 |
与方程
-
=2等价的方程是( )
| (x+2)2+y2 |
| (x-2)2+y2 |
A、x2-
| ||
B、x2-
| ||
C、y2-
| ||
D、x2-
|
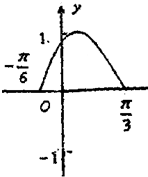 已知函数f(x)=sin(ωx+φ)(其中ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(其中ω>0,|φ|< 如图,正六边形ABCDEF中,已知
如图,正六边形ABCDEF中,已知