题目内容
数列2，5，8，11，…，则23是这个数列的（ ）
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
考点：数列的概念及简单表示法
专题：计算题,等差数列与等比数列
分析：求出数列的通项公式，即可得到结论．
解答：
解：数列2，5，8，11，…，组成以2为首项，3为公差的等差数列，
通项为an=3n-1，
令3n-1=23，可得n=8．
故选：D．
通项为an=3n-1，
令3n-1=23，可得n=8．
故选：D．
点评：本题主要考查数列的概念和简单表示，求出数列的通项公式是解决本题的关键．
练习册系列答案
相关题目
对a、b∈R，记max{a， b}=
，设f1（x）=|x-1|，f2(x)=-x2+6x-5，函数g（x）=max{f1（x），f2（x）}，若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（ ）
|
| A、[1，+∞） | ||
B、[
| ||
C、[
| ||
| D、（3，4） |
定义在（0，π）上的函数f（x）满足f′（x）•sinx＜f（x）•cosx，则下列不等式正确的是（ ）
A、f（
| ||||||||
B、
| ||||||||
| C、sin2•f（1）＜sin1•f（2） | ||||||||
D、sin1•f（
|
若数列{an}的前n项和Sn=3n2-10n，则数列的前10项中正数项的和为（ ）
| A、106 | B、208 |
| C、216 | D、118 |
与方程
-
=2等价的方程是（ ）
| (x+2)2+y2 |
| (x-2)2+y2 |
A、x2-
| ||
B、x2-
| ||
C、y2-
| ||
D、x2-
|
要做一个圆锥形的漏斗，其母线长为40cm，要使其体积为最大，则高为（ ）
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
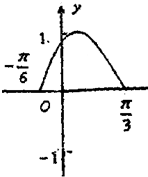已知函数f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜