题目内容
已知a，b，c是非零实数，且a2+b2+c2=1．
（1）证明：
+
+
≥36；
（2）若不等式
+
+
≥|m|+|m-2|对一切a，b，c恒成立，求实数m的取值范围．
（1）证明：
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
（2）若不等式
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
考点：不等式的证明,基本不等式
专题：选作题,不等式
分析：（1）由柯西不等式可得（
+
+
）（a2+b2+c2）≥（1+2+3）2，即可证明结论；
（2）利用（1）的结论，可得|m|+|m-2|≤36，即可求实数m的取值范围．
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
（2）利用（1）的结论，可得|m|+|m-2|≤36，即可求实数m的取值范围．
解答：
（1）证明：由柯西不等式可得（
+
+
）（a2+b2+c2）≥（1+2+3）2，
∴
+
+
≥
，
∵a2+b2+c2=1，
∴
+
+
≥36；
（2）解：∵不等式
+
+
≥|m|+|m-2|对一切a，b，c恒成立，
∴由（1）可得|m|+|m-2|≤36，
∴m＜0时，-m-m+2≤36，∴m≥-17，∴-17≤m＜0；
0≤m≤2时，m-m+2≤36恒成立；
m＞2时，m+m-2≤36，∴m≤19，∴2＜m≤19，
综上，-17≤m≤19．
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
| 36 |
| a2+b2+c2 |
∵a2+b2+c2=1，
∴
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
（2）解：∵不等式
| 1 |
| a2 |
| 4 |
| b2 |
| 9 |
| c2 |
∴由（1）可得|m|+|m-2|≤36，
∴m＜0时，-m-m+2≤36，∴m≥-17，∴-17≤m＜0；
0≤m≤2时，m-m+2≤36恒成立；
m＞2时，m+m-2≤36，∴m≤19，∴2＜m≤19，
综上，-17≤m≤19．
点评：本题考查不等式的证明，考查柯西不等式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
定义在（0，π）上的函数f（x）满足f′（x）•sinx＜f（x）•cosx，则下列不等式正确的是（ ）
A、f（
| ||||||||
B、
| ||||||||
| C、sin2•f（1）＜sin1•f（2） | ||||||||
D、sin1•f（
|
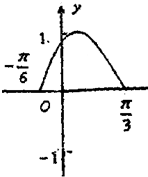已知函数f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜