题目内容
圆O的半径为2，△ABC是其内接三角形，BC=3，则
2-
2的最大值为（ ）
| AC |
| AB |
| A、6 | B、9 | C、10 | D、12 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，过点O作OD⊥BC，垂足为D点，可得
•
=0．利用向量的三角形法则和平行四边形法则可得：
+
=2
，
-
=
，
=
+
．再利用数量积运算即可得出．
| OD |
| BC |
| AB |
| AC |
| AD |
| AC |
| AB |
| BC |
| AD |
| AO |
| OD |
解答：
解：如图所示，
过点O作OD⊥BC，垂足为D点，则
•
=0．
则
+
=2
，
-
=
，
=
+
．
∴
2-
2=(
+
)•(
-
)
=2
•
=2(
+
)•
=2
•
+2
•
=2
•
=2|
| |
|cos＜
，
＞
=2×2×3cos＜
，
＞
≤12，当
∥
且同向时取等号．
因此
2-
2的最大值为12．
故选：D．
过点O作OD⊥BC，垂足为D点，则
| OD |
| BC |
则
| AB |
| AC |
| AD |
| AC |
| AB |
| BC |
| AD |
| AO |
| OD |
∴
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
=2
| AD |
| BC |
=2(
| AO |
| OD |
| BC |
=2
| AO |
| BC |
| OD |
| BC |
=2
| AO |
| BC |
=2|
| AO |
| BC |
| AO |
| BC |
=2×2×3cos＜
| AO |
| BC |
≤12，当
| AO |
| BC |
因此
| AC |
| AB |
故选：D．
点评：本题考查了向量的三角形法则和平行四边形法则、数量积运算等基础知识与基本技能方法，考查了推理能力和辅助线的作法，属于难题．
练习册系列答案
相关题目
设m、n是两条不同的直线，α、β是两个不同的平面．下列四个命题中，正确的是（ ）
| A、α∥β，m?α，n?β，则m∥n |
| B、α⊥β，m⊥β，则m∥α或m?α |
| C、α⊥β，m?α，n?β，则m⊥n |
| D、α∥β，m⊥β，n⊥α，则m∥n |
设正项等比数列{an}的前n项和为Sn，公比为q，若Sk-2=3，Sk=15，Sk+2=63，则q=（ ）
| A、-2 | B、2 | C、-4 | D、4 |
已知函数f(x)=
，且函数h（x）=f（x）+x-a有且只有一个零点，则实数a的取值范围是（ ）
|
| A、[1，+∞） |
| B、（1，+∞） |
| C、（-∞，1） |
| D、（-∞，1] |
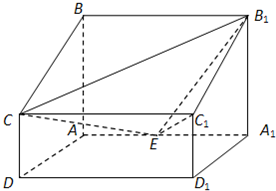四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA1=AB=2，E为AA1的中点．