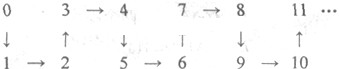题目内容

在△OAB中，∠AOB=120°，OA=OB=2
3
，边AB的四等分点分别为A1，A2，A3，A1靠近A，执行如图算法后结果为
 
．
考点：程序框图
专题：算法和程序框图
分析：根据程序框图进行运行，得到不满足条件的取值，即可得到结论．
解答： 解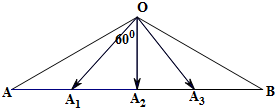：∵△OAB中，∠AOB=120°，OA=OB=2
3
，
∴AA2=3，AA1=
3
2
，AA3=
9
2
，OA2=
3
，
则由余弦定理可得OA=
21
2
，
则cos∠AOA3=
(2
3
)2+(
21
2
)2-(
9
2
)2
2×2
3
×
21
2
=
12+
21
4
-
81
4
6
7
=
-3
6
7
=-
1
2
7
＜0，
∴三次运行的结果是S=
OA1
•
OA
+
OA2
•
OA
+
OA3
•
OA
=（
OA1
+
OA2
+
OA3
）•
OA
=3
OA2
•
OA
=3×
3
×2
3
×
1
2
=9，
故答案为：9．
点评：本题主要考查程序框图的应用和识别，根据向量积的定义和运算性质，以及余弦定理是解决本题的关键，综合性较强，难度较大．
练习册系列答案
相关题目
圆O的半径为2，△ABC是其内接三角形，BC=3，则
AC
2-
AB
2的最大值为（　　）
A、6B、9C、10D、12
（1）已知|x-4|+|3-x|＜a若不等式的解集为空集，求a的范围
（2）已知a，b，c∈R+，且a+b+c=1，求证：a2+b2+c2≥
1
3
．
把命题“?x0∈R，x02-2x0+1＜0”的否定写在横线上
 
．
记Sk=1k+2k+3k+…+nk，当k=1，2，3，…时，观察下列等式：
S1=
1
2
n2+
1
2
n，
S2=
1
3
n3+
1
2
n2+
1
6
n，
S3=
1
4
n4+
1
2
n3+
1
4
n2，
S4=
1
5
n5+
1
2
n4+
1
3
n3-
1
30
n，
S5=
1
6
n6+
1
2
n5+
5
12
n4+An2
，…
可以推测，A=
 
．
已知向量
a
=(cosx，sinx)，
b
=(
2
，
2
)，
a
•
b
=
8
5
，且
π
4
＜x＜
π
2
，则cos(x+
π
4
)的值为
 
．
已知实数x，y满足
y≥1 
y≤2x-1 
x+y≤m 
  
，如果目标函数z=x-y的最小值是-1，那么此目标函数的最大值是
 
．
n个连续自然数按规律排成下表，根据规律，从2012到2014的箭头方向依次为
 
．
①↓→；②→↑；③↑→；④→↓
定义在R上的偶函数f（x）满足f（x+1）f（x）=-2（f（x）≠0），且在区间（2013，2014）上单调递增，已知α，β是锐角三角形的两个内角，则f（sinα）、f（cosβ）的大小关系是（　　）
A、f（sinα）＜f（cosβ）
B、f（sinα）＞f（cosβ）
C、f（sinα）=f（cosβ）
D、以上情况均有可能

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网