题目内容
6．已知正方体ABCD-A′B′C′D′，记过点A与三条直线AB，AD，AA′所成角都相等的直线条数为m，过点A与三个平面AB′，AC，AD′所成角都相等的直线的条数为n，则下面结论正确的是（ ）| A． | m=1，n=1 | B． | m=4，n=1 | C． | m=3，n=4 | D． | m=4，n=4 |
分析 由已知条件结合正方体的结构特征求解．
解答 
解：正方体ABCD-A′B′C′D′，
过点A与三条直线AB，AD，AA′所成角都相等的直线有：AC′，
过A作BD′的平行线，过A作A′C的平行线、过A作B′D的平行线，共4条，故m=4；
过点A与三个平面AB′，AC，AD′所成角都相等的直线分两类：
第一类：通过点A位于三条棱之间的直线有一条体对角线AC1，
第二类：在图形外部和每面所成角和另两个面所成角相等，有3条，合计4条，故n=4．
故选：D．
点评 本题考查满足条件的直线条数的求法，是中档题，解题时要认真审题，注意正方体的结构特征的合理运用．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
16．
某四面体的三视图如图所示，正视图与俯视图都是斜边长为2的等腰直角三角形，左视图是两直角边长为1的三角形，该四棱锥的表面积是（ ）
某四面体的三视图如图所示，正视图与俯视图都是斜边长为2的等腰直角三角形，左视图是两直角边长为1的三角形，该四棱锥的表面积是（ ）| A． | $1+\sqrt{3}$ | B． | $1+2\sqrt{2}$ | C． | $2+\sqrt{3}$ | D． | 2$\sqrt{2}$ |
17．定义在R上的函数y=f（x）是奇函数，且x≥0时，f（x）=ln（x2-2x+2），则x＜0时，f（x）的解析式是（ ）
| A． | f（x）=ln（-x2-2x+2） | B． | f（x）=ln（x2+2x+2） | C． | f（x）=-ln（-x2-2x+2） | D． | f（x）=-ln（x2+2x+2） |
14．点P（2，0）关于直线x+y+1=0对称点Q的坐标为（ ）
| A． | （-1，-3） | B． | （3，3） | C． | （-1，3） | D． | （4，-2） |
11．
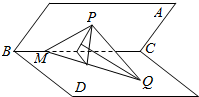如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）
如图所示，二面角A-BC-D的大小为45°，P为平面ABC内一点，Q为平面BCD内一点，M为BC上一点，已知P在平面BCD内的射影恰好在线段MQ上，设PM=$\sqrt{2}$，∠CMQ=45°，直线PQ与平面BCD所成的角为30°，则PQ的长为（ ）| A． | $\frac{2}{3}\sqrt{6}$ | B． | $\frac{3}{4}\sqrt{6}$ | C． | $\frac{4}{3}\sqrt{2}$ | D． | $\frac{3}{2}\sqrt{2}$ |
15．已知点C（3，4），抛物线y2=8x的准线为L，设抛物线上任意一点P到直线L的距离为m，则m+|PC|的最小值为（ ）
| A． | 5 | B． | $\sqrt{41}$ | C． | $\sqrt{41}$-2 | D． | 4 |