题目内容
16. 某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )
某四面体的三视图如图所示,正视图与俯视图都是斜边长为2的等腰直角三角形,左视图是两直角边长为1的三角形,该四棱锥的表面积是( )| A. | $1+\sqrt{3}$ | B. | $1+2\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 由题意作直观图,从而确定每一个三角形的面积即可.
解答 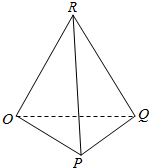 解:由题意作直观图如右图,
解:由题意作直观图如右图,
底面是等腰直角三角形,
故S△OPQ=$\frac{1}{2}$×2×1=1,
侧面ORQ为等腰直角三角形,
故S△ORQ=$\frac{1}{2}$×2×1=1,
侧面ORP与RQP全等,
且为边长为$\sqrt{2}$的正三角形,
∴S△OPR=S△RPQ
=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$×sin60°=$\frac{\sqrt{3}}{2}$,
故表面积S=1+1+2×$\frac{\sqrt{3}}{2}$=2+$\sqrt{3}$,
故选:C.
点评 本题考查了学生的空间想象力与作图能力.

练习册系列答案
相关题目
4.集合$\left\{{x∈N|\frac{6}{x}∈N}\right\}$的真子集有( )个.
| A. | 8 | B. | 16 | C. | 15 | D. | 14 |
11.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | 若α,β不平行,则在α内不存在与β平行的直线 | |
| B. | 若n,m不平行,则n与m不可能垂直于同一个平面 | |
| C. | 若α,β垂直于同一个平面,则α与β平行 | |
| D. | 若n,m平行于同一个平面,则n与m平行 |
6.已知正方体ABCD-A′B′C′D′,记过点A与三条直线AB,AD,AA′所成角都相等的直线条数为m,过点A与三个平面AB′,AC,AD′所成角都相等的直线的条数为n,则下面结论正确的是( )
| A. | m=1,n=1 | B. | m=4,n=1 | C. | m=3,n=4 | D. | m=4,n=4 |