题目内容
20.已知函数f(x)=-ax5-x3+bx-7,若f(2)=-9,则f(-2)=-5.分析 令g(x)=-ax5-x3+bx,则g(2)=-2,又 g(x)为奇函数,故有g(-2)=2,f(-2)=g(-2)-7=-5.
解答 解:∵函数f(x)=-ax5-x3+bx-7,f(2)=-9,
令g(x)=-ax5-x3+bx,则g(2)=-2,
又g(x)为奇函数,∴g(-2)=2,故 f(-2)=g(-2)-7=-5,
故答案为-5.
点评 本题考查函数的奇偶性的应用,求函数值,令g(x)=-ax5-x3+bx,求出g(2)=-2是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
11.下列命题中为真命题的是( )
| A. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| B. | 若直线x-ay=0与直线x-ay=0互相垂直,则a=1 | |
| C. | 命题:“若x2=1,则x=1或x=-1”的逆否命题为:“若x≠1,且x≠-1,则x2≠1” | |
| D. | 一个命题的否命题为真,则它的逆否命题一定为真 |
8.已知$a={2^{\frac{1}{2}}},b={({2^{{{log}_2}^3}})^{-\frac{1}{2}}}$,c=cos50°cos10°+cos140°sin170°,则实数a,b,c的大小关系是( )
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | c>b>a |
12.已知球O的半径为2,四点S、A、B、C均在球O的表面上,且SC=4,AB=$\sqrt{3}$,∠SCA=∠SCB=$\frac{π}{6}$,则点B到平面SAC的距离为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
9.要得到函数f(x)=cos2x的图象,只需将函数g(x)=sin2x的图象( )
| A. | 向左平移$\frac{1}{2}$个周期 | B. | 向右平移$\frac{1}{2}$个周期 | ||
| C. | 向左平移$\frac{1}{4}$个周期 | D. | 向右平移$\frac{1}{4}$个周期 |
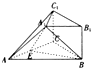 用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD中点,M是棱PC上的点,AD=2BC.