题目内容
12.已知球O的半径为2,四点S、A、B、C均在球O的表面上,且SC=4,AB=$\sqrt{3}$,∠SCA=∠SCB=$\frac{π}{6}$,则点B到平面SAC的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
分析 过AB的小圆的圆心为D.可得AC=BC=2$\sqrt{3}$,AD=BD=$\sqrt{3}$,即可求解B到平面SAC的距离.
解答 解:球的直径SC=4,A,B是该球球面上的两点,AB=$\sqrt{3}$,∠SCA=∠SCB=$\frac{π}{6}$,半径为2,
过AB的小圆的圆心为D.可得AC=BC=2$\sqrt{3}$,AD=BD=$\sqrt{3}$,
∴△ABD是等边三角形,AD边上的高为B到平面SAC的距离,即$\frac{3}{2}$.
故选:B.
点评 本题考查了学生的空间想象力,考查转化思想以及计算能力.属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
2.函数f(x)=ln(1-5x)的定义域是( )
| A. | (-∞,0) | B. | (0,1) | C. | (-∞,1) | D. | (0,+∞) |
17.已知i为虚数单位,则z=i+i2+i3+…+i2017=( )
| A. | 0 | B. | 1 | C. | -i | D. | i |
2.已知O为坐标原点,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,双曲线C上一点P满足($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,且|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=2a2,则双曲线C的渐近线方程为( )
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2x |
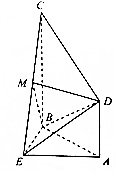 如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.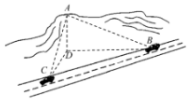 如图,小明同学在山顶A处观测到,一辆汽车在一条水平的公路上沿直线匀速行驶,小明在A处测得公路上B,C两点的俯角分别为30°,45°,且∠BAC=135°.若山高AD=100m,汽车从B点到C点历时14s,则这辆汽车的速度为22.6m/s(精确到0.1)参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236.
如图,小明同学在山顶A处观测到,一辆汽车在一条水平的公路上沿直线匀速行驶,小明在A处测得公路上B,C两点的俯角分别为30°,45°,且∠BAC=135°.若山高AD=100m,汽车从B点到C点历时14s,则这辆汽车的速度为22.6m/s(精确到0.1)参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236.