Question

已知函数f（x）=

ax+b

x2+1

（a＞0）
（1）若函数f（x）的极大值为2，极小值为-2，试求a，b的值；
（2）在（1）的条件下，若函数g（x）=k（x-

1

3

），试讨论函数F（x）=f（x）-g（x）的零点个数．

Answer 1

考点：利用导数研究函数的极值,利用导数研究函数的单调性

专题：计算题,数形结合,导数的综合应用

分析：（1）求出导数f′（x），设x₁，x₂是-ax²-2bx+a=0的两根，且x₁＜x₂，运用韦达定理，及f（x₁）=-2，f（x₂）=2．化简即可求出a，b；
（2）讨论k=0，k＜0，k＞0，设直线与曲线相切的切点为（s，t），由相切的条件，列出方程，解出k=

48

25

，再分①0＜k＜

48

25

，②k=

48

25

，③k＞

48

25

讨论图象的交点个数，即有零点个数．

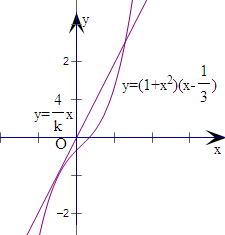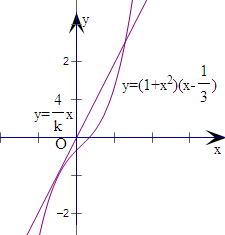解答： 解：（1）f′（x）=

a(x2+1)-2x(ax+b)

(x2+1)2

=

-ax2-2bx+a

(x2+1)2

，（a＞0）
设x₁，x₂是-ax²-2bx+a=0的两根，且x₁＜x₂，
则x₁+x₂=-

2b

a

，x₁x₂=-1，
由于f（x₁）=-2，f（x₂）=2．即

ax1+b

x12+1

=-2，

ax2+b

x22+1

=2可化为

bx12-ax1

x12+1

=2，
则ax₁+b=ax₁-bx₁²，得b=0，x₁+x₂=0，x₁=-1，x₂=1．则a=4，
故a=4，b=0；
（2）f（x）=

4x

1+x2

，令F（x）=f（x）-g（x）=0，即有

4x

1+x2

=k（x-

1

3

），
当k=0，x=0，有一个零点；当k≠0时，

4x

k

=（1+x²）（x-

1

3

）．
当k＜0，y=

4

k

x和y=（1+x²）（x-

1

3

）的图象只有一个交点，即有一个零点；
当k＞0时，设直线与曲线相切的切点为（s，t），
则3s²-

2

3

s+1=

4

k

，t=

4

k

s，t=（1+s²）（s-

1

3

）
化简得，6s³-s²+1=0，得到s=-

1

2

，k=

48

25

，
①当0＜k＜

48

25

时，图象有3个交点，函数有3个零点；
②当k=

48

25

时，图象有2个交点，函数有2个零点；
③当k＞

48

25

时，图象有1个交点，函数有1个零点；
综上，当k≤0或k＞

48

25

时，有1个零点；
当k=

48

25

时，函数有2个零点；
当0＜k＜

48

25

时，函数有3个零点．

点评：本题考查函数的导数的综合运用：求切线和求极值，考查分类讨论和数形结合的数学思想方法，运算求解的能力，属于中档题．