题目内容
光线经过一层玻璃，其强度要损失掉10%，把n块玻璃重叠在一起，通过它的强度减弱到原来的
以下，则n满足的关系式为（ ）
| 1 |
| 3 |
A、（1-10%）n-1＜
| ||
B、（1-10%）n＜
| ||
C、（1-10%）n+1＜
| ||
D、（1+10%）n＜
|
考点：有理数指数幂的化简求值
专题：计算题,应用题,函数的性质及应用
分析：设光线原来的强度为aa，通过n块玻璃后强度为y，得到y=a（1-10%）n，由通过n块玻璃的强度减弱到原来的
以下即可得到不等式（1-10%）n＜
．
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：设光线原来的强度为a，通过n块玻璃后强度为y．
则y=a（1-10%）n，
要使通过它的强度减弱到原来的
以下，
则a（1-10%）n＜
a，
即（1-10%）n＜
．
故选：B．
则y=a（1-10%）n，
要使通过它的强度减弱到原来的
| 1 |
| 3 |
则a（1-10%）n＜
| 1 |
| 3 |
即（1-10%）n＜
| 1 |
| 3 |
故选：B．
点评：本题考查了有理指数幂的运算性质，考查了数学建模思想方法，是基础题．
练习册系列答案
相关题目
设
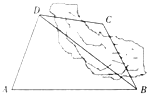如图，为了计算某湖岸边两景点B与C的距离，由于地形的限制，需要岸上A和D两个测量点，现测得AD⊥CD，AD=10km，AB=14km，∠BDA=60°，∠BCD=135°，则两景点B与C之间的距离为（假设A，B，C，D在同一平面内）（ ）| A、16km | ||
B、8
| ||
C、16
| ||
| D、8km |
不等式（a-1）x2+（a-1）x+1＞0在x∈R时恒成立，则a的取值范围是（ ）
| A、[1，5] |
| B、[1，5） |
| C、（-∞，1） |
| D、（3，+∞） |
已知数列{an}和{bn}满足：a1=1，a2=2，an＞0，bn=
，且{bn}是以
为公比的等比数列，若cn=a2n-1+2a2n，则数列{cn}的前n项和为（ ）
| anan+1 |
| 2 |
| A、5×2n-5 |
| B、3×2n-3 |
| C、2n+1-2 |
| D、2n-1 |
若0＜x＜
，则x与2sinx的大小关系为（ ）
| π |
| 3 |
| A、x＞2sinx |
| B、x=2sinx |
| C、x＜2sinx |
| D、与x值有关 |