题目内容
关于函数f(x)=sinxcosx-cos2x,给出下列命题:
①f(x)的最小正周期为2π;
②f(x)在区间(0,
)上为增函数;
③直线x=
是函数f(x)图象的一条对称轴;
④函数f(x)的图象可由函数f(x)=
sin2x的图象向右平移
个单位得到;
⑤对任意x∈R,恒有f(
+x)+f(-x)=-1.
其中正确命题的序号是 .
①f(x)的最小正周期为2π;
②f(x)在区间(0,
| π |
| 8 |
③直线x=
| 3π |
| 8 |
④函数f(x)的图象可由函数f(x)=
| ||
| 2 |
| π |
| 8 |
⑤对任意x∈R,恒有f(
| π |
| 4 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:三角函数的图像与性质,简易逻辑
分析:利用降幂把三角函数解析式化为y=Asin(ωx+φ)+k的形式,然后直接由周期公式求周期判断①;
求出三角函数的增区间判断②;把x=
代入函数f(x)的解析式求解函数值判断③;利用函数图象的平移求得函数解析式判断④;直接代入验证判断⑤.
求出三角函数的增区间判断②;把x=
| 3π |
| 8 |
解答:
解:函数f(x)=sinxcosx-cos2x
=
sin2x-
=
(sin2x-cos2x)-
=
sin(2x-
)-
.
∴T=π.
∴命题①错误;
由-
+2kπ≤2x-
≤
+2kπ,k∈Z.
解得:-
+kπ≤x≤
+kπ,k∈Z.
取k=0,得-
≤x≤
.
∴f(x)在区间(0,
)上为增函数.
∴命题②正确;
取x=
,得f(x)=
sin(2×
-
)-
=
为函数的最大值,
∴直线x=
是函数f(x)图象的一条对称轴.
∴命题③正确;
函数f(x)=
sin2x的图象向右平移
个单位,得到f(x)=
sin2(x-
)=
sin(2x-
).
∴命题④错误;
对任意x∈R,f(
+x)+f(-x)=
sin[2×(
+x)-
]-
+
sin(-2x-
)-
=
sin(2x+
)+
sin(-2x-
)-1=-1.
∴命题⑤正确.
∴正确命题的序号是②③⑤.
故答案为:②③⑤.
=
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴T=π.
∴命题①错误;
由-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得:-
| π |
| 8 |
| 3π |
| 8 |
取k=0,得-
| π |
| 8 |
| 3π |
| 8 |
∴f(x)在区间(0,
| π |
| 8 |
∴命题②正确;
取x=
| 3π |
| 8 |
| ||
| 2 |
| 3π |
| 8 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
∴直线x=
| 3π |
| 8 |
∴命题③正确;
函数f(x)=
| ||
| 2 |
| π |
| 8 |
| ||
| 2 |
| π |
| 8 |
| ||
| 2 |
| π |
| 4 |
∴命题④错误;
对任意x∈R,f(
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
∴命题⑤正确.
∴正确命题的序号是②③⑤.
故答案为:②③⑤.
点评:本题考查命题的真假判断与应用,综合考查三角恒等变换、三角函数的性质,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知三个正数a,b,c,满足b<a+c≤2b,a<b+c≤2a,则
的取值范围是( )
| a |
| b |
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
△ABC外接圆半径等于1,其圆心O满足
=
(
+
),|
|=|
|,则向量
在
方向上的投影等于( )
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AC |
| BA |
| BC |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、3 |
 如图是正方体的平面展开图,在这个正方体中,以下四个命题:
如图是正方体的平面展开图,在这个正方体中,以下四个命题: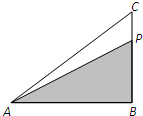 如图,在Rt△ABC中,AB=4,BC=3,点P在边BC上沿B→C运动,则△ABP的面积小于4的概率为
如图,在Rt△ABC中,AB=4,BC=3,点P在边BC上沿B→C运动,则△ABP的面积小于4的概率为