题目内容
△ABC外接圆半径等于1，其圆心O满足
=
(
+
)，|
|=|
|，则向量
在
方向上的投影等于（ ）
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AC |
| BA |
| BC |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、3 |
考点：平面向量数量积的含义与物理意义
专题：平面向量及应用
分析：由△ABC外接圆圆心O满足
=
(
+
)，可得点O在BC上．由于|
|=|
|．可得△OAC是等边三角形．可得|
|=|
|sin60°，进而得到向量
在
方向上的投影=|
|cos30°．
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| AC |
| AB |
| BC |
| BA |
| BC |
| BA |
解答：
解：△ABC外接圆半径等于1，其圆心O满足
=
(
+
)，
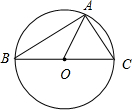
∴点O在BC上，∴∠BAC=90°．
∵|
|=|
|．
∴△OAC是等边三角形．
∴∠ACB=60°．
∴|
|=|
|sin60°=
．
∴向量
在
方向上的投影=|
|cos30°=
×
=
．
故选：C．
| AO |
| 1 |
| 2 |
| AB |
| AC |
∴点O在BC上，∴∠BAC=90°．
∵|
| AO |
| AC |
∴△OAC是等边三角形．
∴∠ACB=60°．
∴|
| AB |
| BC |
| 3 |
∴向量
| BA |
| BC |
| BA |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
故选：C．
点评：本题考查了三角形外接圆的性质、含30°的直角三角形的边角关系、等边三角形的定义、向量的投影等基础知识与基本技能方法，属于中档题．
练习册系列答案
相关题目
已知椭圆在区间[0，4]内随机取两个实数a，b，则使得方程x2+ax+b2=0有实根的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知正方形ABCD，AB=2，AC、BD交点为O，在ABCD内随机取一点E，则点E满足OE＜1的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={x∈R|-1≤x≤1}，B={x∈R|x（x-3）≤0}，则A∩B等于（ ）
| A、{x∈R|-1≤x≤3} |
| B、{x∈R|0≤x≤3} |
| C、{x∈R|-1≤x≤0} |
| D、{x∈R|0≤x≤1} |
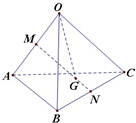已知空间四边形OABC，其对角线为OB，AC，M，N分别是边OA，BC的中点，点G在线段MN上，若MG=λGN，且