题目内容
(理科学生做)已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn),(n为正整数)都在函数y=(
)x的图象上.
(1)若数列{an}是等差数列,求证:数列{bn}是等比数列;
(2)设an=n(n∈N*),过点An(an+2,0),Bn(0,(n+2)bn+1)的直线与两坐标轴所围成的三角形面积为cn,试求最小的实数t,使cn≤t对一切正整数n恒成立;
(3)对(2)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},设Sn是数列{dn}的前n项和,试探究2014是否是数列{Sn}中的某一项,写出你探究得到的结论并给出证明.
| 1 |
| 2 |
(1)若数列{an}是等差数列,求证:数列{bn}是等比数列;
(2)设an=n(n∈N*),过点An(an+2,0),Bn(0,(n+2)bn+1)的直线与两坐标轴所围成的三角形面积为cn,试求最小的实数t,使cn≤t对一切正整数n恒成立;
(3)对(2)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},设Sn是数列{dn}的前n项和,试探究2014是否是数列{Sn}中的某一项,写出你探究得到的结论并给出证明.
考点:数列与函数的综合
专题:综合题,等差数列与等比数列
分析:(1)根据题中已知条件以及等差数列的基本性质,先求出bn的通项公式,然后证明为常数即可证明;
(2)先求出bn的通项公式,然后求出cn的表达式,可知数列cn随n增大而减小,故c1≤t,便可求出t的最小值;
(3)根据题意先求出dn的表达式,然后求出Sn的表达式,因为2014-1120=894=298×3,是3的倍数,所以存在自然数m,使Sm=2014.
(2)先求出bn的通项公式,然后求出cn的表达式,可知数列cn随n增大而减小,故c1≤t,便可求出t的最小值;
(3)根据题意先求出dn的表达式,然后求出Sn的表达式,因为2014-1120=894=298×3,是3的倍数,所以存在自然数m,使Sm=2014.
解答:
解:(1)设等差数列的公差为d,则
由已知bn=(
)an,∵数列{an}是等差数列,
∴
=(
)d(常数),
∴数列{bn}是等比数列.
(2)∵an=n,∴bn=(
)n
∴cn=(n+2)2•(
)n+2,
∴
=
<1,
∴数列{cn}随n增大而减小,
∵cn≤t对一切正整数n恒成立
∴c1≤t,
∴t≥
,
∴最小的实数t为
;
(3))∵an=n,∴数列{dn}中,从第一项a1开始到ak为止(含ak项)的所有项的和是(1+2+…+k)+(31+32+…+3k-1)=
+
,
当k=7时,其和是28+
=1120<2014,而当k=8时,其和是36+
=3315>2014,
又∵2014-1120=894=298×3,是3的倍数,
所以存在自然数m,使Sm=2014.
此时m=7+(1+3+32+…+35)+298=669.
由已知bn=(
| 1 |
| 2 |
∴
| bn+1 |
| bn |
| 1 |
| 2 |
∴数列{bn}是等比数列.
(2)∵an=n,∴bn=(
| 1 |
| 2 |
∴cn=(n+2)2•(
| 1 |
| 2 |
∴
| cn+1 |
| cn |
| (n+3)2 |
| 2(n+2)2 |
∴数列{cn}随n增大而减小,
∵cn≤t对一切正整数n恒成立
∴c1≤t,
∴t≥
| 9 |
| 8 |
∴最小的实数t为
| 9 |
| 8 |
(3))∵an=n,∴数列{dn}中,从第一项a1开始到ak为止(含ak项)的所有项的和是(1+2+…+k)+(31+32+…+3k-1)=
| k(k+1) |
| 2 |
| 3k-3 |
| 2 |
当k=7时,其和是28+
| 37-3 |
| 2 |
| 38-3 |
| 2 |
又∵2014-1120=894=298×3,是3的倍数,
所以存在自然数m,使Sm=2014.
此时m=7+(1+3+32+…+35)+298=669.
点评:本题考查了等差数列和等比数列的基本性质以及函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
球面上有M、N两点,在过M、N的球的大圆上,
的度数为90°,在过M、N的球小圆上,
的度数为120°,又MN=
cm,则球心到上述球小圆的距离是( )
 |
| MN |
 |
| MN |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
设点P(x,y),其中x,y∈N,则满足x+y≤3的点P的个数为( )
| A、10 | B、9 | C、3 | D、无数 |
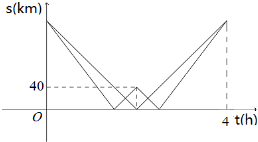 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行 如图,已知椭圆E:
如图,已知椭圆E: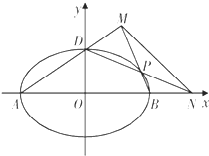 已知椭圆
已知椭圆