题目内容
已知三个正数a,b,c,满足b<a+c≤2b,a<b+c≤2a,则
的取值范围是( )
| a |
| b |
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
考点:其他不等式的解法,简单线性规划
专题:不等式的解法及应用
分析:将不等式进行转化,利用不等式的性质建立关于
的不等式关系,即可得到结论.
| b |
| a |
解答:
解:∵三个正数a,b,c,满足b<a+c≤2b,a<b+c≤2a,
∴1<
+
≤2,
<1+
≤
,
即-
≤-1-
<-
,
不等式的两边同时相加得1-
<
-1<2-
,
则等价为
,
即
,
即
<
<
,
即
<
<
,
故选:A.
∴1<
| b |
| a |
| c |
| a |
| b |
| a |
| c |
| a |
| 2b |
| a |
即-
| 2b |
| a |
| c |
| a |
| b |
| a |
不等式的两边同时相加得1-
| 2b |
| a |
| b |
| a |
| b |
| a |
则等价为
|
即
|
即
| 2 |
| 3 |
| b |
| a |
| 3 |
| 2 |
即
| 2 |
| 3 |
| a |
| b |
| 3 |
| 2 |
故选:A.
点评:本题主要考查不等式的解法,利用不等式的性质将不等式进行转化是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
在区间[0,4]内随机取两个实数a,b,则使得方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知正方形ABCD,AB=2,AC、BD交点为O,在ABCD内随机取一点E,则点E满足OE<1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
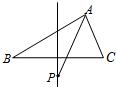 如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则
如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则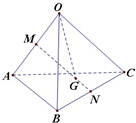 已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且
已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且