题目内容
已知a=cos2
-sin2
，b=sin1，c=
，则a，b，c的大小关系是（ ）
| π |
| 6 |
| π |
| 6 |
| tan30° |
| 1-tan230° |
| A、a＜b＜c |
| B、a＞b＞c |
| C、c＞a＞b |
| D、a＜c＜b |
考点：二倍角的余弦,二倍角的正切
专题：三角函数的求值
分析：利用二倍角公式求出a、c的值，根据正弦函数的定义域和值域求得b的范围，可得a，b，c的大小关系．
解答：
解：∵a=cos2
-sin2
=cos
=
，
b=sin1∈（
，
），
c=
=
×
=
tan
=
，
∴c＞b＞a，
故选：A．
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
b=sin1∈（
| ||
| 2 |
| ||
| 2 |
c=
| tan30° |
| 1-tan230° |
| 1 |
| 2 |
| 2tan30° |
| 1-tan230° |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴c＞b＞a，
故选：A．
点评：本题主要考查二倍角公式的应用，正弦函数的定义域和值域，属于基础题．
练习册系列答案
相关题目
用4种不同的颜色给图中A、B、C、D四个区域涂色，要求相邻的区域涂色不同，则不同的涂色方法共有已知
=（2，-2
），
=（-7，0），则
与
的夹角为（ ）
| a |
| 3 |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
如图所示，不等式x（y-x-1）＞0 表示的平面区域是（ ）
A、 |
B、 |
C、 |
D、 |
若ax（1+
）5的展开式中x2项的系数是20，则实数a等于（ ）
| x |
| A、2 | B、3 | C、4 | D、5 |
已知随机变量X～N（4，1），且P（3≤X≤5）=0.6826，则P（X＜3）等于（ ）
| A、0.1585 |
| B、0.1586 |
| C、0.1587 |
| D、0.1588 |
在△ABC中，若对任意的λ∈R，都有|
+λ
|≥|
|，则△ABC（ ）
| AB |
| AC |
| BC |
| A、一定为锐角三角形 |
| B、一定为钝角三角形 |
| C、一定为直角三角形 |
| D、可以为任意三角形 |
已知Rt△ABC中，∠C=90°，AB=5，BC=4，以BC为直径的圆交AB于D，则BD的长为（ ）
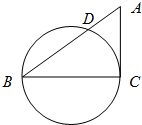
| A、4 | ||
B、
| ||
C、
| ||
D、
|
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
