题目内容
已知sin(x-45°)=
,求
(1)sinxcosx的值;
(2)tanx+
.
| ||
| 4 |
(1)sinxcosx的值;
(2)tanx+
| 1 |
| tanx |
考点:两角和与差的正弦函数,三角函数的化简求值
专题:三角函数的求值
分析:(1)利用两角和差的正弦公式展开,平方即可sinxcosx的值;
(2)将tanx+
进行化简即可.
(2)将tanx+
| 1 |
| tanx |
解答:
解:(1)sin(x-45°)=sinxcos45°-cosxsin45°=
(sinx-cosx)=
,
即sinx-cosx=
,
平方得1-2sinxcosx=
,
则sinxcosx=
.
(2)tanx+
=
+
=
=
=
.
| ||
| 2 |
| ||
| 4 |
即sinx-cosx=
| 1 |
| 2 |
平方得1-2sinxcosx=
| 1 |
| 4 |
则sinxcosx=
| 3 |
| 8 |
(2)tanx+
| 1 |
| tanx |
| sinx |
| cosx |
| cosx |
| sinx |
| sin2x+cos2x |
| sinxcosx |
| 1 |
| sinxcosx |
| 8 |
| 3 |
点评:本题主要考查三角函数值的求解,将三角函数式进行化简是解决本题的关键.

练习册系列答案
相关题目
已知集合P={x|0≤x≤4},集合N={y|0≤y≤2},下列从P到Q的各对应关系f不是函数的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
空间四边形ABCD中,若AD⊥BC,AD⊥BD,那么有( )
| A、平面ABC⊥平面ADC |
| B、平面ABC⊥平面ADB |
| C、平面ABC⊥平面DBC |
| D、平面ADC⊥平面DBC |
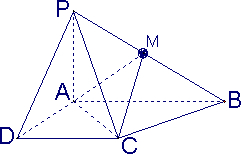 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=