题目内容
已知抛物线y2=4x,点M(1,0)关于y轴的对称点为N,直线l过点M交抛物线于A,B两点,
(1)证明:直线NA,NB的斜率互为相反数;
(2)求△ANB面积的最小值.
(1)证明:直线NA,NB的斜率互为相反数;
(2)求△ANB面积的最小值.
考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)如图所示,设直线l的方程为:x=my+1,A(x1,y1),B(x2,y2).与抛物线方程联立可得根与系数的关系,利用斜率计算公式可得kNA=
,kNB=
,只有证明kNA+kNB=0即可.
(2)利用S△ANB=
|MN||y1-y2|=|y1-y2|=
=
即可得出.
| y1 |
| x1+1 |
| y2 |
| x2+1 |
(2)利用S△ANB=
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
| 16m2+16 |
解答:
(1)证明:如图所示,
设直线l的方程为:x=my+1,A(x1,y1),B(x2,y2).
联立
,化为y2-4my-4=0,△>0,
∴y1+y2=4m,y1y2=-4.
kNA=
,kNB=
,
∴kNA+kNB=
+
=
=
=
=0,
∴直线NA,NB的斜率互为相反数.
(2)解:S△ANB=
|MN||y1-y2|=|y1-y2|=
=
≥4,
当且仅当m=0时取等号.
∴当AB⊥x轴时,△ANB面积取得最小值4.

设直线l的方程为:x=my+1,A(x1,y1),B(x2,y2).
联立
|
∴y1+y2=4m,y1y2=-4.
kNA=
| y1 |
| x1+1 |
| y2 |
| x2+1 |
∴kNA+kNB=
| y1 |
| x1+1 |
| y2 |
| x2+1 |
| y1(x2+1)+y2(x1+1) |
| (x1+1)(x2+1) |
| 2my1y2+2(y1+y2) |
| (x1+1)(x2+1) |
| -8m+8m |
| (x1+1)(x2+1) |
∴直线NA,NB的斜率互为相反数.
(2)解:S△ANB=
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
| 16m2+16 |
当且仅当m=0时取等号.
∴当AB⊥x轴时,△ANB面积取得最小值4.
点评:本题考查了直线与抛物线相交转化为方程联立可得根与系数的关系、斜率计算公式、三角形的面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(2,1)+f(1,2)=( )
| A、45 | B、60 | C、96 | D、108 |

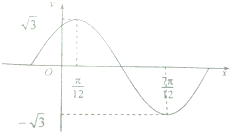 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<