题目内容
已知函数f(x)=2asin(2x-
)+b的定义域为[0,
],值域为[-5,1],求a和b的值.
| π |
| 3 |
| π |
| 2 |
考点:正弦函数的定义域和值域
专题:分类讨论,三角函数的图像与性质
分析:由x的取值范围,求出2x-
的取值范围,从而求出sin(2x-
)的取值范围;讨论a>0、a<0时,函数f(x)的最值问题,从而求出a和b的值.
| π |
| 3 |
| π |
| 3 |
解答:
解:∵0≤x≤
,∴0≤2x≤π,
∴-
≤2x-
≤π-
,
即-
≤2x-
≤
π,
∴-
≤sin(2x-
)≤1;
当a>0时,则
,解得
;
当a<0时,则
,解得
;
∴a=12-6
,b=-23+12
或a=-12+6
,b=19-12
.
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
即-
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
当a>0时,则
|
|
当a<0时,则
|
|
∴a=12-6
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了三角函数的图象与应用问题,解题时应根据三角函数的最值与值域的关系,利用分类讨论的方法,求出a和b的值.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
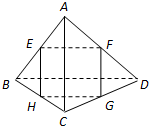 如图,空间四边形ABCD中,E,F,G,H分别为BA,AD,DC,CB边上的中点.则下列说法中不正确的是( )
如图,空间四边形ABCD中,E,F,G,H分别为BA,AD,DC,CB边上的中点.则下列说法中不正确的是( )| A、四边形EFGH为平行四边形 |
| B、直线AC∥平面EFGH |
| C、若棱AC=BD,则四边形EFGH为矩形 |
| D、若棱AC=BD,则四边形EFGH为菱形 |