题目内容
 如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,
如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,(1)求证:AC1∥平面CDB1;
(2)求二面角B-B1C-D的正弦值的大小.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连接BC1交B1C于E,证明AC1∥平面CDB1,只需证明AC1∥DE,利用三角形中位线可得;
(2)求出点B到平面B1CD的距离,即可求二面角B-B1C-D的正弦值的大小.
(2)求出点B到平面B1CD的距离,即可求二面角B-B1C-D的正弦值的大小.
解答:
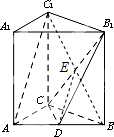 (1)证明:连接BC1交B1C于E,∴E为BC1的中点,…(2分)
(1)证明:连接BC1交B1C于E,∴E为BC1的中点,…(2分)
连接DE,由D为AB的中点,∴DE为△ABC1的中位线,
∴AC1∥DE,…(4分)
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1; …(6分)
(2)解:由AC=BC=C1C易知BB1C1C为正方形,
∴BE⊥B1C,
令AC=BC=C1C=1,
设点B到平面B1CD的距离为d,则由等体积可得
•
•
•
d=
•
•
•
•1,
∴点B到平面B1CD的距离为
,且BE=
,…(10分)
若二面角B-B1C-D的平面角为α,则sinα=
=
.…(12分)
 (1)证明:连接BC1交B1C于E,∴E为BC1的中点,…(2分)
(1)证明:连接BC1交B1C于E,∴E为BC1的中点,…(2分)连接DE,由D为AB的中点,∴DE为△ABC1的中位线,
∴AC1∥DE,…(4分)
∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1; …(6分)
(2)解:由AC=BC=C1C易知BB1C1C为正方形,
∴BE⊥B1C,
令AC=BC=C1C=1,
设点B到平面B1CD的距离为d,则由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴点B到平面B1CD的距离为
| ||
| 3 |
| ||
| 2 |
若二面角B-B1C-D的平面角为α,则sinα=
| d |
| BE |
| ||
| 3 |
点评:本题考查线面平行,考查面面角,正确利用线面平行的判定定理,求出点B到平面B1CD的距离是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
大小为-
的角的终边落在( )
| 11π |
| 4 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
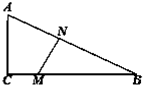 有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?
有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?