题目内容
若斜率为k的两条平行直线l,m与曲线C相切并至少有两个切点,且曲线C上的所有点都在l,m之间(也可在直线l,m上),则把l,m称为曲线C的“夹线”,把l,m间的距离称为曲线C在“k方向上的宽度”,记为d(k).已知函数f(x)=x+3cosx.
(Ⅰ)若点P横坐标为0,求f(x)图象在点P处的切线方程;
(Ⅱ)试判断y=x+3和y=x-3是否是f(x)的“夹线”,若是,求d(1);若不是,请说明理由;
(Ⅲ)求证:函数F(x)=-
x3+x的图象不存在“夹线”.
(Ⅰ)若点P横坐标为0,求f(x)图象在点P处的切线方程;
(Ⅱ)试判断y=x+3和y=x-3是否是f(x)的“夹线”,若是,求d(1);若不是,请说明理由;
(Ⅲ)求证:函数F(x)=-
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出函数f(x)的导函数,得到f′(0),再求出f(0)的值,然后由直线方程的点斜式得f(x)图象在点P处的切线方程;
(Ⅱ)由(Ⅰ)知y=x+3是f(x)图象在点P处的切线,再由导函数的值等于1可求得另外至少一个切点(2π,2π+3),同理得到满足斜率为-1的曲线的切点至少有两个(π,π-3),(3π,3π-3),然后利用作差法结合三角函数的值域说明曲线f(x)夹在两直线y=x+3和y=x-3之间.由两平行线间的距离公式求得d(1);
(Ⅲ)设出F(x)=-
x3+x上的任意一点,求出曲线在该点处的切线方程,和y=-
x3+x联立后解得两交点坐标,再由曲线在求得的两点出的导数值相等得到切点唯一,不符合曲线存在夹线的条件,说明函数F(x)=-
x3+x的图象不存在“夹线”.
(Ⅱ)由(Ⅰ)知y=x+3是f(x)图象在点P处的切线,再由导函数的值等于1可求得另外至少一个切点(2π,2π+3),同理得到满足斜率为-1的曲线的切点至少有两个(π,π-3),(3π,3π-3),然后利用作差法结合三角函数的值域说明曲线f(x)夹在两直线y=x+3和y=x-3之间.由两平行线间的距离公式求得d(1);
(Ⅲ)设出F(x)=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
(Ⅰ)解:由f(x)=x+3cosx,得
f′(x)=1-3sinx,
∴k=f′(0)=1-3sin0=1,
又f(0)=0+3cos0=3,
∴P点坐标为p(0,3),
∴f(x)图象在点P处的切线方程是y-3=x-0,即y=x+3;
(Ⅱ)解:y=x+3和y=x-3是f(x)的“夹线”.
由(Ⅰ)知y=x+3是f(x)图象在点P处的切线,切点为(0,3).
∵f′(x)=1-3sinx=1,
∴sinx=0.
当x=2π时,y=2π+3,f(2π)=2π+3cos2π=2π+3,
∴(2π,2π+3)是函数y=x+3和f(x)=x+3cosx图象的另一个切点.
y=x+3和f(x)=x+3cosx的图象相切且至少有两个切点.
同理,(π,π-3),(3π,3π-3)是y=x-3和f(x)=x+3cosx图象的两个切点.
因此,两条平行直线与曲线相切并至少有两个切点.
令g(x)=x+3,h(x)=x-3.
对任意x∈R,g(x)-f(x)=(x+3)-(x+3cosx)=3-3cosx≥0,
∴g(x)≥f(x).
h(x)-f(x)=(x-3)-(x+3cosx)=-3-3cosx≤0,
∴h(x)≤f(x).
y=x+3和y=x-3是f(x)的“夹线”
∴d(1)=
=3
;
(Ⅲ)证明:设F(x)=-
x3+x的图象上任一点为P(x0,y0),
∴F′(x)=-x2+1,k=F′(x0)=-x02+1,
又F(x0)=-
x03+x0,
∴F(x)在点P(x0,y0)处的切线方程为y-(-
x03+x0)=(-x02+1)(x-x0),
即y=(-x02+1)x+
x03.
联立
,得-
x3+x=(-x02+1)x+
x03,
∴(x-x0)2(x+2x0)=0,解得:x=x0或x=-2x0.
∴k=F′(x0)=-x02+1,
k′=F′(-2x0)=-(-2x0)2+1=-4x02+1,
∴k=k′时,当且仅当x0=0时取到,此时切线与F(x)=-
x3+x的图象只有一个交点.
∴F(x)=-
x3+x的图象和它在任一点处的切线至多只有一个切点.
∴函数F(x)=-
x3+x的图象不存在“夹线”.
f′(x)=1-3sinx,
∴k=f′(0)=1-3sin0=1,
又f(0)=0+3cos0=3,
∴P点坐标为p(0,3),
∴f(x)图象在点P处的切线方程是y-3=x-0,即y=x+3;
(Ⅱ)解:y=x+3和y=x-3是f(x)的“夹线”.
由(Ⅰ)知y=x+3是f(x)图象在点P处的切线,切点为(0,3).
∵f′(x)=1-3sinx=1,
∴sinx=0.
当x=2π时,y=2π+3,f(2π)=2π+3cos2π=2π+3,
∴(2π,2π+3)是函数y=x+3和f(x)=x+3cosx图象的另一个切点.
y=x+3和f(x)=x+3cosx的图象相切且至少有两个切点.
同理,(π,π-3),(3π,3π-3)是y=x-3和f(x)=x+3cosx图象的两个切点.
因此,两条平行直线与曲线相切并至少有两个切点.
令g(x)=x+3,h(x)=x-3.
对任意x∈R,g(x)-f(x)=(x+3)-(x+3cosx)=3-3cosx≥0,
∴g(x)≥f(x).
h(x)-f(x)=(x-3)-(x+3cosx)=-3-3cosx≤0,
∴h(x)≤f(x).
y=x+3和y=x-3是f(x)的“夹线”
∴d(1)=
| |3-(-3)| | ||
|
| 2 |
(Ⅲ)证明:设F(x)=-
| 1 |
| 3 |
∴F′(x)=-x2+1,k=F′(x0)=-x02+1,
又F(x0)=-
| 1 |
| 3 |
∴F(x)在点P(x0,y0)处的切线方程为y-(-
| 1 |
| 3 |
即y=(-x02+1)x+
| 2 |
| 3 |
联立
|
| 1 |
| 3 |
| 2 |
| 3 |
∴(x-x0)2(x+2x0)=0,解得:x=x0或x=-2x0.
∴k=F′(x0)=-x02+1,
k′=F′(-2x0)=-(-2x0)2+1=-4x02+1,
∴k=k′时,当且仅当x0=0时取到,此时切线与F(x)=-
| 1 |
| 3 |
∴F(x)=-
| 1 |
| 3 |
∴函数F(x)=-
| 1 |
| 3 |
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了数学转化思想方法,解答此题的关键在于对新定义的理解,是压轴题.

练习册系列答案
相关题目
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为( )
| α |
A、
| ||
B、
| ||
C、
| ||
D、
|
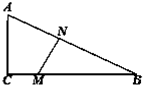 有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?
有一块实验题,形如图的直角△ABC,其中∠C=90°,AC=50米,BC=120米,拟在边BC和BA之间开出一条水渠,即图示中线段MN,并且使这条水渠恰好能平分该实验题的面积.为节省人力、物力,要使这条水渠最短.问:应如何设计?水渠最短的长度为多少米?