题目内容
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为
.过F1的直线L交C于A,B两点,且△ABF的周长为16,那么C的方程( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据题意,△ABF2的周长为16,即BF2+AF2+BF1+AF1=16,结合椭圆的定义,有4a=16,即可得a的值;又由椭圆的离心率,可得c的值,进而可得b的值;由椭圆的焦点在x轴上,可得椭圆的方程.
解答:
解:根据题意,△ABF2的周长为16,即BF2+AF2+BF1+AF1=16;
根据椭圆的性质,有4a=16,即a=4;
椭圆的离心率为
,即
=
,则a=
c,
将a=
c,代入可得,c=2
,则b2=a2-c2=8;
则椭圆的方程为
+
=1;
故选:D.
根据椭圆的性质,有4a=16,即a=4;
椭圆的离心率为
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
将a=
| 2 |
| 2 |
则椭圆的方程为
| x2 |
| 16 |
| y2 |
| 8 |
故选:D.
点评:本题考查椭圆的性质,此类题型一般与焦点三角形联系,难度一般不大;注意结合椭圆的基本几何性质解题即可.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知为虚数单位,a为实数,复数z=(a-2i)(1+i)在复平面内对应的点为M,则“a=2”是“点M在坐标轴上”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
下列函数中,在区间(0,+∞)上是增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-3x-2 | ||
D、y=(
|
设f(x)与g(x)是定义在R上的两个函数,若对任意x∈[a,b],都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“密切函数”.若f(x)=x2-3x+4与g(x)=2x+t在[2,3]上时“密切函数”,则实数t的取值范围是( )
| A、[-3,-1] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-3,-
|
已知函数f(x)定义域为R,f′(x)存在,且f(-x)=f(x),则f′(0)=( )
| A、2 | B、1 | C、0 | D、-1 |
 某同学在研究函数f(x)=
某同学在研究函数f(x)=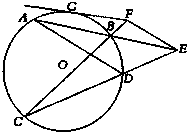 已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.
已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.