题目内容
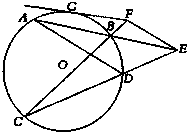已知：如图，圆O两弦AB与CD交于E，EF∥AD，EF与CB延长线交于F，FG切圆O于G．（Ⅰ）求证：△BEF∽△CEF；
（Ⅱ）求证：FG=EF．
考点：相似三角形的判定,与圆有关的比例线段
专题：直线与圆
分析：（1）由EF∥AD，∠BEF=∠DAB=∠ECF，又∠EFB=∠CFE，由此能证明△BEF∽△CEF．
（2）由△BEF∽△CEF，得EF2=CF×BF，由切割线定理得FG2=FB×FC，由此能证明EF=FG．
（2）由△BEF∽△CEF，得EF2=CF×BF，由切割线定理得FG2=FB×FC，由此能证明EF=FG．
解答：
证明：（1）∵EF∥AD，
∴∠BEF=∠DAB=∠ECF，
∵∠EFB=∠CFE，
∴△BEF∽△CEF．
（2）∵△BEF∽△CEF，
∴
=
，
∴EF2=CF×BF，
∵FG切圆于G，
∴FG2=FB×FC，
∴EF2=FG2，即，EF=FG．
∴∠BEF=∠DAB=∠ECF，
∵∠EFB=∠CFE，
∴△BEF∽△CEF．
（2）∵△BEF∽△CEF，
∴
| EF |
| CF |
| BF |
| EF |
∴EF2=CF×BF，
∵FG切圆于G，
∴FG2=FB×FC，
∴EF2=FG2，即，EF=FG．
点评：本题考查三角形相似的证明，考查线段长相等的证明，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
相关题目
已知0＜a＜1，在同一坐标系中作出两个函数的图象（如图），那么这两个函数可以为（ ）| A、y=ax和y=loga（-x） |
| B、y=a-x和y=loga（-x） |
| C、y=ax和y=logax-1 |
| D、y=a-x和y=logax-1 |
在平面直角坐标系xOy中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为
．过F1的直线L交C于A，B两点，且△ABF的周长为16，那么C的方程（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|