题目内容
计算:1+cos(
+α)•sin(
-α)•tan(π+α)= .
| π |
| 4 |
| π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:由条件利用诱导公式、两角和差的余弦公式化简所给式子,可得结果.
解答:
解:1+cos(
+α)•sin(
-α)•tan(π+α)=1+cos(
+α)•cosα•tanα=1+cos(
+α)•sinα=1+(
cosα-
sinα)sinα
=1+
sin2α-
•
=1-
+
sin2α+
cos2α=1-
+
sin(2α+
),
故答案为:1-
+
sin(2α+
).
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
=1+
| ||
| 4 |
| ||
| 2 |
| 1-cos2α |
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| π |
| 4 |
故答案为:1-
| ||
| 4 |
| 1 |
| 2 |
| π |
| 4 |
点评:本题主要考查两角和的余弦公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
三菱锥S-ABC是正三菱锥,则A在侧面SBC上的射影H必为△SBC的( )
| A、外心 | B、内心 | C、垂心 | D、重心 |
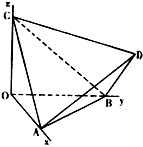 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A、O-ABC是正三棱锥 |
| B、直线AD与OB所成的角是45° |
| C、直线OB∥平面ACD |
| D、二面角D-OB-A为45° |