题目内容
现有六名篮球运动员进行传球训练,由甲开始传球(第一次传球是由甲传向其他五名运动员中的一位),若第n次传球后,球传回到甲的不同传球方式的种数记为an.
(1)求出a1、a2的值,并写出an与an-1(n≥2)的关系式;
(2)证明数列{
-
}是等比数列,并求出数列{an}的通项公式;
(3)当n≥2时,证明:
+
+…+
<
.
(1)求出a1、a2的值,并写出an与an-1(n≥2)的关系式;
(2)证明数列{
| an |
| 5n |
| 1 |
| 6 |
(3)当n≥2时,证明:
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 3 |
| 10 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)第n-1次传球后,不同传球方式种数为5n-1,不在甲手中的种数为5n-1-an-1,由此能求出a1、a2的值,并写出an与an-1(n≥2)的关系式.
(2)由an=-an-1+5n-1,得
-
=-
(
-
),由此能证明数列{
-
}是以-
为首项,-
为公比的等比数列,从而能求出an=
.
(3)当n(n≥3)为奇数时,则n-1为偶数,
+
=
+
=
[1-(
)n-1]<
;当n(n≥2)为偶数时,则n+1为奇数,从而(
+
)…+(
+
)<
,由此能证明当n≥2时,
+
…+
<
.
(2)由an=-an-1+5n-1,得
| an |
| 5n |
| 1 |
| 6 |
| 1 |
| 5 |
| an-1 |
| 5n-1 |
| 1 |
| 6 |
| an |
| 5n |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 5 |
| 5n+5(-1)n |
| 6 |
(3)当n(n≥3)为奇数时,则n-1为偶数,
| 1 |
| an-1 |
| 1 |
| an |
| 6 |
| 5n-1+5 |
| 6 |
| 5n-5 |
| 3 |
| 10 |
| 1 |
| 5 |
| 3 |
| 10 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
| 3 |
| 10 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 3 |
| 10 |
解答:
(本小题满分13分)
(1)解:a1=0,a2=5,
第n-1次传球后,不同传球方式种数为5n-1,
不在甲手中的种数为5n-1-an-1,
∴当n≥2时,an=5n-1-an-1…(5分)
(2)解:由an=-an-1+5n-1,得
-
=-
(
-
),
又
-
=-
,
则数列{
-
}是以-
为首项,-
为公比的等比数列.
从而
-
=-
•(-
)n-1,
故an=
.…(9分)
(3)证明:当n(n≥3)为奇数时,则n-1为偶数,
+
=
+
=6•
=6•
<6•
=6(
+
)
+
…+
=(
+
)+…+(
+
)
<6[(
+
)+…+(
+
)]
=6
=
[1-(
)n-1]<
当n(n≥2)为偶数时,则n+1为奇数,
从而(
+
)…+(
+
)<
综上,当n≥2时,
+
…+
<
.…(13分)
(1)解:a1=0,a2=5,
第n-1次传球后,不同传球方式种数为5n-1,
不在甲手中的种数为5n-1-an-1,
∴当n≥2时,an=5n-1-an-1…(5分)
(2)解:由an=-an-1+5n-1,得
| an |
| 5n |
| 1 |
| 6 |
| 1 |
| 5 |
| an-1 |
| 5n-1 |
| 1 |
| 6 |
又
| a1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
则数列{
| an |
| 5n |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 5 |
从而
| an |
| 5n |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 5 |
故an=
| 5n+5(-1)n |
| 6 |
(3)证明:当n(n≥3)为奇数时,则n-1为偶数,
| 1 |
| an-1 |
| 1 |
| an |
| 6 |
| 5n-1+5 |
| 6 |
| 5n-5 |
=6•
| 5n-1+5n |
| 5n-1•5n+5•5n-5•5n-1-25 |
=6•
| 5n-1+5n |
| 5n-1•5n+4•5n-25 |
<6•
| 5n-1+5n |
| 5n-1•5n |
=6(
| 1 |
| 5n-1 |
| 1 |
| 5n |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
=(
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
| 1 |
| an |
<6[(
| 1 |
| 52 |
| 1 |
| 53 |
| 1 |
| 5n-1 |
| 1 |
| 5n |
=6
| ||||
1-
|
| 3 |
| 10 |
| 1 |
| 5 |
| 3 |
| 10 |
当n(n≥2)为偶数时,则n+1为奇数,
从而(
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
| 3 |
| 10 |
综上,当n≥2时,
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 3 |
| 10 |
点评:本题考查an与an-1(n≥2)的关系式的求法,考查数列{
-
}是等比数列,考查数列{an}的通项公式的求法,考查不等式的证明,注意构造法的合理运用.
| an |
| 5n |
| 1 |
| 6 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=lnx-
(x>0,a∈R).
(1)试求f(x)的单调区间;
(2)是否存在正实数a,使得函数y=f(x)的图象存在唯一零点?若存在,试求出a的取值集合,若不存在,试说明理由.
| a(x-1) |
| x |
(1)试求f(x)的单调区间;
(2)是否存在正实数a,使得函数y=f(x)的图象存在唯一零点?若存在,试求出a的取值集合,若不存在,试说明理由.
圆x2+y2-6x+7=0上的点到直线x-y+1=0距离的最小值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、3
|
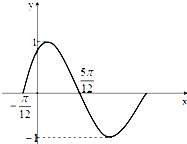 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<