题目内容
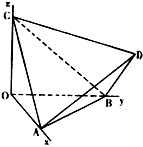 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A、O-ABC是正三棱锥 |
| B、直线AD与OB所成的角是45° |
| C、直线OB∥平面ACD |
| D、二面角D-OB-A为45° |
考点:异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:结合图形,逐一分析答案,运用排除、举反例直接计算等手段,找出正确答案.
解答:
解:A.∵AB2=OA2+OB2,BC2=OB2+OC2,
AC2=OA2+OC2,AB=BC=CA,
∴OA=OB=OC.∴O-ABC是正三棱锥,A正确;
B.如图所示,∵AE∥OB,∠DAE=45°,
∴异面直线AD与OB所成的角为45°,因此B正确;
C.将正四面体ABCD放入正方体中,
如图所示,显然OB与平面ACD不平行.
则C不正确;
D.由右图可知,BE⊥OB,OB⊥DB,
则∠EBD即为二面角D-OB-A的平面角,且为45°,则D正确.
故选C.
AC2=OA2+OC2,AB=BC=CA,
∴OA=OB=OC.∴O-ABC是正三棱锥,A正确;

B.如图所示,∵AE∥OB,∠DAE=45°,
∴异面直线AD与OB所成的角为45°,因此B正确;
C.将正四面体ABCD放入正方体中,
如图所示,显然OB与平面ACD不平行.
则C不正确;
D.由右图可知,BE⊥OB,OB⊥DB,
则∠EBD即为二面角D-OB-A的平面角,且为45°,则D正确.
故选C.
点评:结合图形分析答案,增强直观性,考查空间想象能力.属中档题.

练习册系列答案
相关题目
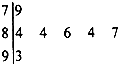 如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、84,4.84 |
| B、84,1.6 |
| C、85,1.6 |
| D、85,4 |
圆x2+y2-6x+7=0上的点到直线x-y+1=0距离的最小值为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、3
|
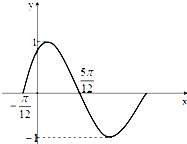 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<