题目内容
若关于x的一元二次方程x2-4x+k-1=0的两个实数根为x1,x2,且满足x1=2x2,试求出方程的两个实数根及k的值.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:利用根与系数的关系公式,构成方程组解之.
解答:
解:由已知x1+x2=4,x1x2=k-1,x1=2x2,
所以x2=
,x1=
,k=x1x2-1=
-1=
.
所以x2=
| 4 |
| 3 |
| 8 |
| 3 |
| 32 |
| 9 |
| 23 |
| 9 |
点评:本题考查了一元二次方程根与系数的关系运用,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
函数f(x)=lnx-
(x>0,a∈R).
(1)试求f(x)的单调区间;
(2)是否存在正实数a,使得函数y=f(x)的图象存在唯一零点?若存在,试求出a的取值集合,若不存在,试说明理由.
| a(x-1) |
| x |
(1)试求f(x)的单调区间;
(2)是否存在正实数a,使得函数y=f(x)的图象存在唯一零点?若存在,试求出a的取值集合,若不存在,试说明理由.
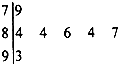 如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A、84,4.84 |
| B、84,1.6 |
| C、85,1.6 |
| D、85,4 |

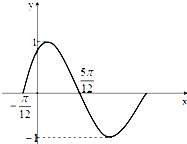 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ<