题目内容
已知f（x）的定义域为[a，b]，b＞-a＞0，f（-x）的定义域为 ，f（x）-f（-x）的定义域为 ．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由已知中f（x）的定义域为[a，b]，令a≤-x≤b，可得f（-x）的定义域，进而根据若f（x）-f（-x）有意义，则a≤x≤b且-b≤x≤-a，得到f（x）-f（-x）的定义域．
解答：
解：∵f（x）的定义域为[a，b]，
令a≤-x≤b得：-b≤x≤-a，
故f（-x）的定义域为：[-b，-a]，
若f（x）-f（-x）有意义，则a≤x≤b且-b≤x≤-a，
又∵b＞-a＞0，
∴f（x）-f（-x）的定义域为：[a，-a]，
故答案为：[-b，-a]，[a，-a]
令a≤-x≤b得：-b≤x≤-a，
故f（-x）的定义域为：[-b，-a]，
若f（x）-f（-x）有意义，则a≤x≤b且-b≤x≤-a，
又∵b＞-a＞0，
∴f（x）-f（-x）的定义域为：[a，-a]，
故答案为：[-b，-a]，[a，-a]
点评：本题考查的知识点是函数的定义域及其求法，难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设集合M={x|y=
}，集合N={y|y=x2，x∈M}，则M∩N=（ ）
| x-2 |
| A、[2，+∞） |
| B、[4，+∞） |
| C、[0，+∞） |
| D、[0，4] |
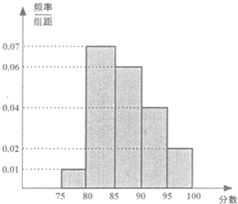一企业某次招聘新员工分笔试和面试两部分，人力资源部经理把参加笔试的40名学生的成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到频率分布直方图如图所示．下列求导函数运算正确的是（ ）
A、（x+
| ||||
B、（
| ||||
| C、[（3+x2）（2-x3）]′=2x（2-x3）-3x2（3+x2） | ||||
| D、（x2•cosx）′=2x•cosx+x2•sinx |
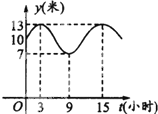某港口水深y（米）是时间t（0≤t≤24，单位：小时）的函数，下表是水深数据：