题目内容
若A(x1,y1)、B(x2,y2)为平面直角坐标系xOy上的两点,定义由A点到B点的一种折线距离ρ(A,B)=|x2-x1|+|y2-y1|.已知点N(1,0),点M为直线3x+4y-5=0上的动点,则ρ(M,N)的最小值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:进行简单的合情推理
专题:计算题,新定义,推理和证明
分析:由折线距离的定义ρ(A,B)=|x1-x2|+|y1-y2|,求出ρ(M,N)的值,通过去绝对值,求得一次函数的值域,再求并集,即可得到最小值.
解答:
解:∵N(1,0),点M为直线3x+4y-5=0上动点,设M(x,y),
则d=ρ(M,N)=|x1-x2|+|y1-y2|=|x-1|+|y|=|x-1|+
|3x-5|
=
,
当x<1时,d>
,当1≤x≤
,
≤d≤
,当x>
,d>
,
则d≥
,
即有最小值为
.
故选B.
则d=ρ(M,N)=|x1-x2|+|y1-y2|=|x-1|+|y|=|x-1|+
| 1 |
| 4 |
=
|
当x<1时,d>
| 1 |
| 2 |
| 5 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 3 |
则d≥
| 1 |
| 2 |
即有最小值为
| 1 |
| 2 |
故选B.
点评:本题是中档题,考查新定义,利用新定义求出函数的最小值问题,考查计算能力,对新定义的理解和灵活运应是解好本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
如图:底面是矩形ABCD,PA⊥底面ABCD,则图中直角三角形的个数( )
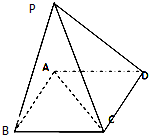

| A、8 | B、7 | C、6 | D、5 |
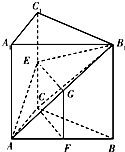 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,