题目内容

已知椭圆两个焦点F1（-c，0）、F2（c，0），P为椭圆一点．且PF1•PF2=c2，则离心率范围
 
．
考点：椭圆的简单性质
专题：
分析：由椭圆的定义得：|PF1|+|PF2|=2a整体求解余弦定理：|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2=|F1F2|2=4c2，整体化简求解．
解答： 解：由椭圆的定义得：|PF1|+|PF2|=2a
平方得：|PF1|2+|PF2|2+2|PF1|•|PF2|=4a2．①
又∵PF1•PF2=c2，∴|PF1|•|PF2|cos∠F1PF2=c2，②
由余弦定理得：
|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2=|F1F2|2=4c2，③
由①②③得：cos∠F1PF2=
c2
2a2-3c2
≤1，
2
c≤a，e≤
2
2

|PF1|•|PF2|=2a2-3c2，又|PF1|•|PF2|≤（
|PF1|+|PF2|
2
）2=a2
∴2a2-3c2≤a2，a2≤3c2
即e≥
3
3

则此椭圆离心率的取值范围是：[
3
3
，
2
2
]
故答案为：[
3
3
，
2
2
]
点评：本题考察了椭圆的定义，三角形中定理，综合运算．
练习册系列答案
相关题目
已知直线AB过抛物线y2=4x的焦点F，交抛物线于A、B两点，点A在x轴的上方，且弦AB的中点为C（2，m），求弦AB的长和m的值．
已知f（x）的定义域为[a，b]，b＞-a＞0，f（-x）的定义域为
 
，f（x）-f（-x）的定义域为
 
．
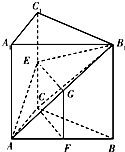如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1的中点，
F是AB的中点，AC=BC=1，AA1=2．
（Ⅰ）求证：CF∥平面AB1E；
（Ⅱ）求三棱锥C-AB1E在底面AB1E上的高．
奇函数f（x）的定义域为R，当x≥0时，f（x）=2x-x2，设函数y=f（x），x∈[a，b]的值域为[
1
a
，
1
b
]（a≠b），求a，b的值．
在正方体ABCD-A1B1C1D1中，E是BB1的中点，O是底面正方形ABCD的中心．求证：OE⊥平面ACD1．
在直角坐标系xOy中 已知椭圆C：
x2
4
+
y2
3
=1上一点P（1，
3
2
），过点P的直线l1，l2与椭圆C分别交于点A、B，且他们的斜率k1，k2满足k1．k2=-
3
4
，求证：
（1）直线AB过定点；
（2）求△PAB面积的最大值．
已知二次函数f（x）=ax2+bx且f（2）=0，方程f（x）-1=0有两个相等的实数根．
（1）求函数f（x）的解析式；
（2）用定义证明f（x）在[1，+∞）上是减函数；
（3）当x∈[-
1
2
，
3
2
]时，利用图象求f（x）的最大值和最小值．
在△ABC中，a=1，b=2，cosC=
1
2
，则c=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网