题目内容
若实数x,y满足
,则z=
的取值范围为 .
|
| y+2 |
| x-1 |
考点:简单线性规划
专题:计算题,不等式的解法及应用
分析:由约束条件作出可行域,然后利用z的几何意义是区域内任意一点(x,y)与点P(1,-2)两点直线的斜率,求解z的范围.
解答:
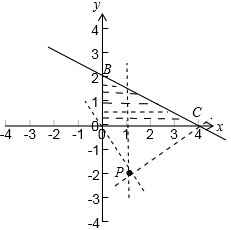 解:作出不等式组对应的平面区域OBC.
解:作出不等式组对应的平面区域OBC.
因为z=
,
所以z的几何意义是区域内任意一点(x,y)与点P(1,-2)两点直线的斜率.
所以由图象可知当直线经过点P,C时,斜率为正值中的最小值,
经过点P,O时,直线斜率为负值中的最大值.
由题意知C(4,0),所以kOP=-2,kPC=
=
,
所以z=
的取值范围为z≥
或z≤-2,
即(-∞,-2]∪[
,+∞).
故答案为:(-∞,-2]∪[
,+∞).
 解:作出不等式组对应的平面区域OBC.
解:作出不等式组对应的平面区域OBC.因为z=
| y+2 |
| x-1 |
所以z的几何意义是区域内任意一点(x,y)与点P(1,-2)两点直线的斜率.
所以由图象可知当直线经过点P,C时,斜率为正值中的最小值,
经过点P,O时,直线斜率为负值中的最大值.
由题意知C(4,0),所以kOP=-2,kPC=
| -2-0 |
| 1-4 |
| 2 |
| 3 |
所以z=
| y+2 |
| x-1 |
| 2 |
| 3 |
即(-∞,-2]∪[
| 2 |
| 3 |
故答案为:(-∞,-2]∪[
| 2 |
| 3 |
点评:本题考查了简单的线性规划,考查了数形结合的解题思想,解答的关键是理解z=
几何意义,是中档题.
| y+2 |
| x-1 |

练习册系列答案
相关题目
已知集M={x|y=
},N={x|x=t2,t∈M},则集合M∩N等于( )
| 1-x2 |
| A、M | B、N | C、R | D、ϕ |
设a,b为实数,则“a>b>0是
<
”的( )
| 1 |
| a |
| 1 |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
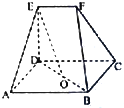 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=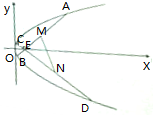 已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点.
已知点E(m,0)为抛物线y2=4x内的一个定点,过E作斜率分别为k1、k2的两条直线交抛物线于点A、B、C、D,且M、N分别是AB、CD的中点.