Question

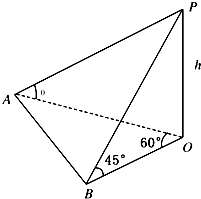地平面上一旗杆OP，为测得它的高度h，在地平面上取一基线AB，AB=30m，在A处测得旗杆顶P点的仰角为θ且tanθ=

1

2

，在B处测得P点的仰角∠OBP=45°，又测得∠AOB=60°，求旗杆的高h．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：分别在直角三角形AOP和直角三角形BDP中，求得OA，OB，进而在△AOB中，由余弦定理求得旗杆的高度．

解答： 解：在直角△AOP中，得OA=2h．
在直角△BOP中，得OB=OPcot45°=h
在△AOB中，由余弦定理得30²=4h²+h²-2•2h•h•cos60°
∴h=10

3

m．

点评：本题主要考查了解三角形的实际应用．考查了学生运用数学知识解决实际问题的能力．