题目内容
已知函数f（x）=（x-1）ex-x2．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）求函数f（x）在区间[0，k]（k＞0）上的最大值．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）求函数f（x）在区间[0，k]（k＞0）上的最大值．
考点：利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题：综合题,导数的概念及应用
分析：（Ⅰ）求导数，利用导数的正负，求函数f（x）的单调区间；
（Ⅱ）分类讨论，即可求函数f（x）在区间[0，k]（k＞0）上的最大值．
（Ⅱ）分类讨论，即可求函数f（x）在区间[0，k]（k＞0）上的最大值．
解答：
解：（Ⅰ）由f′（x）=x（ex-2）＞0，可得x＜0或x＞ln2，
∴函数f（x）的单调增区间为（-∞，0），（ln2，+∞）；
由f′（x）=x（ex-2）＜0，可得0＜x＜ln2，
∴函数f（x）的单调增区间为（0，ln2）；
（Ⅱ）∵f（0）=f（1）=-1，且f（x）在（0，ln2）上递减，在（ln2，1）上递增，
∴0＜k≤1时，f（x）max=f（0）=-1，
k＞1时，f（x）max=f（k）=（k-1）ek-k2．
∴函数f（x）的单调增区间为（-∞，0），（ln2，+∞）；
由f′（x）=x（ex-2）＜0，可得0＜x＜ln2，
∴函数f（x）的单调增区间为（0，ln2）；
（Ⅱ）∵f（0）=f（1）=-1，且f（x）在（0，ln2）上递减，在（ln2，1）上递增，
∴0＜k≤1时，f（x）max=f（0）=-1，
k＞1时，f（x）max=f（k）=（k-1）ek-k2．
点评：本题考查了利用导数求函数的单调区间，考查闭区间上函数的最值，求函数在闭区间[a，b]上的最大值与最小值是通过比较函数在（a，b）内所有极值与端点函数f（a），f（b） 比较而得到的．
练习册系列答案
相关题目
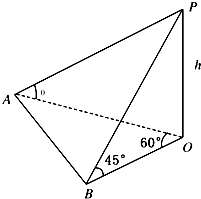地平面上一旗杆OP，为测得它的高度h，在地平面上取一基线AB，AB=30m，在A处测得旗杆顶P点的仰角为θ且tanθ=| 1 |
| 2 |
设a∈R，则“a=1”是“直线l2：ax+y-1=0与直线l2：x-ay-3=0垂直”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |