题目内容
已知a∈R,函数f(x)=ax2+2x-3-a+
,求f(x)在[0,1]上的值域.
| 4 |
| a |
考点:二次函数的性质
专题:分类讨论,函数的性质及应用
分析:本题可以先对二次项系数进行分类讨论,以确定抛物线的开口方向,再对抛物线的对称轴位置进行分类讨论,确定图象特征,得到最值情况,从而得出本题结论.
解答:
解:∵函数f(x)=ax2+2x-3-a+
,
∴a≠0,函数f(x)的图象是抛物线,对称轴方程为x=-
.
(1)当a>0时,-
<0,
∴抛物线开口向上,对称轴在区间左边,函数f(x)在[0,1]上单调递增.
∴f(0)≤f(x)≤f(1),即-3-a+
≤f(x)≤-1+
,
∴函数f(x)在[0,1]上的值域为[-3-a+
,-1+
];
(2)当a<0时,-
>0,
∴抛物线开口向下.
①当0<-
<
,即a<-2时,
抛物线的对称轴在区间[0,1]内偏左,
∴f(1)≤f(x)≤f(-
),即-1+
≤f(x)≤-3-a+
,
∴函数f(x)在[0,1]上的值域为[-1+
,-3-a+
];
②当
≤-
≤1,即-2≤a≤-1时,
抛物线的对称轴在区间[0,1]内偏右,
∴f(0)≤f(x)≤f(-
),即-3-a+
≤f(x)≤-3-a+
,
∴函数f(x)在[0,1]上的值域为[-3-a+
,-3-a+
];
③当-
>1,即-1<a<0时,
抛物线的对称轴在区间[0,1]右,
∴f(0)≤f(x)≤f(1),即-3-a+
≤f(x)≤-1+
,
∴函数f(x)在[0,1]上的值域为[-3-a+
,-1+
].
综上,①当a<-2时,函数f(x)在[0,1]上的值域为[-1+
,-3-a+
];
②当-2≤a≤-1时,函数f(x)在[0,1]上的值域为[-3-a+
,-3-a+
];
③当-1<a<0时,函数f(x)在[0,1]上的值域为[-3-a+
,-1+
];
④当a>0时,函数f(x)在[0,1]上的值域为[-3-a+
,-1+
].
| 4 |
| a |
∴a≠0,函数f(x)的图象是抛物线,对称轴方程为x=-
| 1 |
| a |
(1)当a>0时,-
| 1 |
| a |
∴抛物线开口向上,对称轴在区间左边,函数f(x)在[0,1]上单调递增.
∴f(0)≤f(x)≤f(1),即-3-a+
| 4 |
| a |
| 4 |
| a |
∴函数f(x)在[0,1]上的值域为[-3-a+
| 4 |
| a |
| 4 |
| a |
(2)当a<0时,-
| 1 |
| a |
∴抛物线开口向下.
①当0<-
| 1 |
| a |
| 1 |
| 2 |
抛物线的对称轴在区间[0,1]内偏左,
∴f(1)≤f(x)≤f(-
| 1 |
| a |
| 4 |
| a |
| 1 |
| a |
∴函数f(x)在[0,1]上的值域为[-1+
| 4 |
| a |
| 1 |
| a |
②当
| 1 |
| 2 |
| 1 |
| a |
抛物线的对称轴在区间[0,1]内偏右,
∴f(0)≤f(x)≤f(-
| 1 |
| a |
| 4 |
| a |
| 1 |
| a |
∴函数f(x)在[0,1]上的值域为[-3-a+
| 4 |
| a |
| 1 |
| a |
③当-
| 1 |
| a |
抛物线的对称轴在区间[0,1]右,
∴f(0)≤f(x)≤f(1),即-3-a+
| 1 |
| a |
| 4 |
| a |
∴函数f(x)在[0,1]上的值域为[-3-a+
| 1 |
| a |
| 4 |
| a |
综上,①当a<-2时,函数f(x)在[0,1]上的值域为[-1+
| 4 |
| a |
| 1 |
| a |
②当-2≤a≤-1时,函数f(x)在[0,1]上的值域为[-3-a+
| 4 |
| a |
| 1 |
| a |
③当-1<a<0时,函数f(x)在[0,1]上的值域为[-3-a+
| 1 |
| a |
| 4 |
| a |
④当a>0时,函数f(x)在[0,1]上的值域为[-3-a+
| 4 |
| a |
| 4 |
| a |
点评:本题考查了二次函数的值域求法,还考查了分类讨论的数学思想,本题有一定的思维难度,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
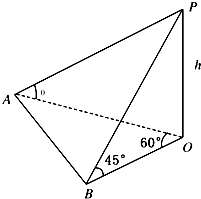 地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=
地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=| 1 |
| 2 |
在同一直角坐标系中,函数f(x)=logax(a>0,a≠1)与函数g(x)=ax(a>0,a≠1)的图象可能是( )
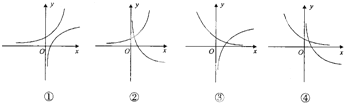

| A、①② | B、①③ | C、①④ | D、②④ |